Высота жидкости в цилиндре равна (8 видео)

Расчет объема жидкости в цилиндрической таре, лежащей на боку (создано по запросу пользователя).

Ага, сегодня я путем несложных умозаключений буду выяснять объем жидкости, находящейся в цилиндрической таре, лежащей на боку.
И это не праздности ради, а дела для.

Цитирую запрос пользователя объем сегмента цилиндра (2):
Доброго времени суток. Видел калькулятор объема сегмента цилиндра, но нужно немножко другое. По работе приходится измерять количество жидкости в таре. Так вот допустим тара цилиндрической формы R=1,13м и H=6,3м лежит на поверхности. Жидкости в таре 0,9м от поверхности. Вопрос: какой объем жидкости в таре?

Там дальше в запросе идут ссылки на решение, но это же не спортивно, поэтому я пошел своим путем ? Сразу замечу, что вторая, более сложная задача — объем жидкости в таре, лежащей под наклоном, еще ждет своего решения.

Вот калькулятор, который все считает, а ход рассуждений, как обычно, под ним.

Содержание

Объем жидкости в цилиндрической таре
Расчет объема жидкости в бочке или цилиндре
Инструкция для калькулятора расчета объема жидкости в бочке
Высота жидкости в цилиндре равна
💥 Видео

Объем жидкости в цилиндрической таре

Итак, сформулируем задачу наглядно, и посмотрим на цилиндр в разрезе (см. рисунок). Если уровень жидкости m больше половины, то находим объем воздуха в оставшейся части, а потом вычитаем из общего объема — т. е. всегда сводим к случаю, изображенному на рисунке.

Формула объема всего цилиндра известна — площадь основания, помноженная на высоту.

А нам, значит, надо найти площадь фигуры, залитой синей жидкостью, и тоже помножить на высоту. Пытливый взгляд отметит, что фигура, залитая синей жидкостью, получается из сектора после вычета верхнего треугольника.

Площадь сектора находится как
, где альфа — это угол дуги в радианах.

Угол дуги нам неизвестен. Разберемся сначала с ним. Линия, опущенная вертикально вниз делит верхний треугольник на два прямоугольных треугольника. Гипотенуза у них равна R, а катет, прилежащий к верхнему углу, равен R-m. Таким образом,

и ответ нам Javascript даст как раз в радианах, то что нам нужно.

Теперь разберемся с верхним треугольником. Он равнобедренный, бедра равны R, а основание нам неизвестно. Найдем его.
А оно как раз равно удвоенному противолежащему катету, который, согласно всем известной теореме Пифагора равен

Зная все стороны треугольника, нетрудно найти его площадь по формуле Герона — Расчет площади треугольника по формуле Герона.

Вот, собственно, и все. Мы знаем площадь сектора и площадь треугольника. Вычитаем площадь треугольника из площади сектора, домножаем на высоту цилиндра (или длину цилиндра, с учетом того, что он лежит) и получаем результат.

Видео:🔴 В сосуде, имеющем форму конуса, уровень жидкости ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Расчет объема жидкости в бочке или цилиндре

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Инструкция для калькулятора расчета объема жидкости в бочке

Впишите размеры неполной вертикальной емкости в миллиметрах:

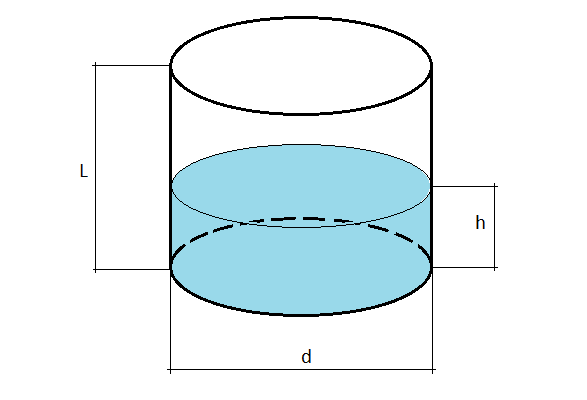
L – Длина резервуара, т.е. линейный размер цистерны в продольном направлении.

d – Диаметр емкости (численно равен двум радиусам).

Параметры L и d можно измерить рулеткой, лазерным дальномером или линейкой.

h – Высота уровня жидкости, ее определяют мерной линейкой (т.н. метршток), если такого инструмента нет, подойдет обычный стержень из проволоки или дерева подходящей длины. Соблюдая меры безопасности, опустите строго вертикально стержень в емкость до дна, отметив уровень, достаньте и измерьте рулеткой. Также определить h можно, измерив, расстояние от верха цистерны до поверхности жидкости и отняв этот показатель от значения диаметра.

Нажмите «Рассчитать».

Онлайн калькулятор поможет посчитать полный объём емкости и узнать максимальное количество жидкости в кубических метрах или литрах, которое может вместить резервуар. Узнать количество жидкости – сколько вещества поместилось в цистерне. Значение свободного объёма даст представление, сколько жидкости еще влезет в емкость. Также программа вычислит площадь дна, площадь боковой поверхности и общую площадь емкости, что поможет легко прикинуть нужное количество покрасочных материалов для обработки всей цистерны или ее частей.

Видео:В первом цилиндрическом сосуде уровень жидкости достигаетСкачать

Высота жидкости в цилиндре равна

В цилиндрическом сосуде уровень жидкости достигает 128 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 8 раз больше первого? Ответ выразите в сантиметрах.

Объем цилиндра выражается через его диаметр и высоту формулой откуда При увеличении диаметра сосуда в восемь раз высота жидкости уменьшится в 64 раза. Поэтому уровень жидкости во втором сосуде будет находиться на высоте см.

В сосуд цилиндрической формы налили воду до уровня 80 см. Какого уровня достигнет вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у первого? Ответ дайте в см.

Читайте также: Расположение цилиндров ситроен с4 ep6

Объём воды, налитой в цилиндр, высотой и радиусом равен Следовательно, при увеличении радиуса цилиндра в 4 раза, при неизменном объёме, высота стола воды окажется в раз меньше, значит, вода во втором цилиндре достигнет уровня 5 см.

Объём воды, налитой в цилиндр, высотой и радиусом равен Следовательно, при увеличении радиуса цилиндра в 4 раза, при неизменном объёме, высота столба воды окажется в раз меньше, значит, вода во втором цилиндре достигнет уровня 5 см.

Вода в сосуде цилиндрической формы находится на уровне h=40 см. На каком уровне окажется вода, если её перелить в другой циллиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте в сантиметрах.

Объём воды, налитой в цилиндр, высотой и радиусом равен Следовательно, при увеличении радиуса цилиндра в 2 раза, при неизменном объёме, высота стола воды окажется в раза меньше, значит, вода во втором цилиндре достигнет уровня 10 см.

Вода в сосуде цилиндрической формы находится на уровне h = 80 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте в сантиметрах.

Объём воды по условию не изменен и вычисляется по формуле: Таким образом, если радиус основания увеличится вдвое, то при неизменном объёме высота уменьшится в раза ().

Вода в сосуде цилиндрической формы находится на уровне см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте в сантиметрах.

Объём первого цилиндра равен объём второго цилиндра равен Так как то

Вода в сосуде цилиндрической формы находится на уровне h = 100 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте в сантиметрах.

Вода в сосуде цилиндрической формы находится на уровне h = 40 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания в полтора раза меньше, чем у данного? Ответ дайте в сантиметрах.

Объём воды, налитой в цилиндр, высотой и радиусом равен Следовательно, при уменьшении радиуса цилиндра в 1,5 раза, при неизменном объёме, высота столба воды окажется в раза больше, значит, вода во втором цилиндре достигнет уровня 90 см.

Вода в сосуде цилиндрической формы находится на уровне h = 80 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания в четыре раза больше, чем у данного? Ответ дайте в сантиметрах.

В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 2 раза больше первого? Ответ выразите в сантиметрах.