Цилиндр (от лат. пер. «цилиндрус«) — каток, валик.
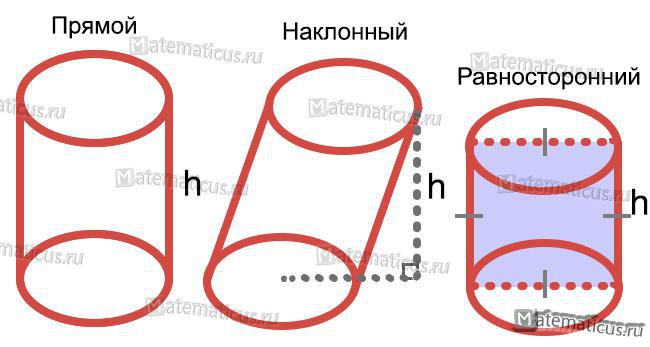
Прямым круговым цилиндром называют часть пространства, заключенной внутри цилиндрической поверхности, лежащей между двумя плоскостями, перпендикулярными образующей.
Равносторонний цилиндр — это цилиндр, у которого диаметр основания равен образующей (то есть осевое сечение — квадрат).
Наклонный цилиндр — это цилиндр, образующие которого не перпендикулярны плоскостям его оснований.
Цилиндр можно получить путём вращения прямоугольника вокруг прямой, содержащей любую его сторону.
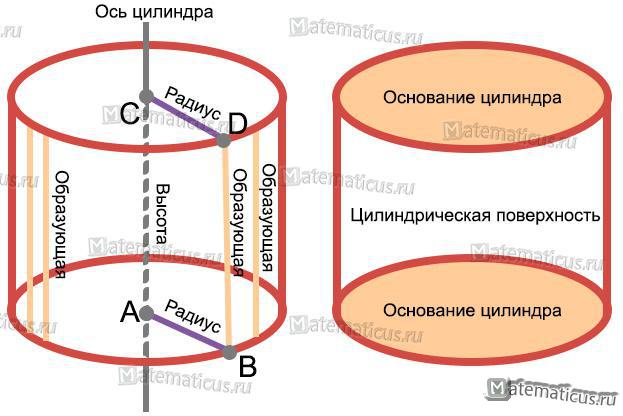
Высотой цилиндра называется расстояние AC между плоскостями его оснований.
Радиус цилиндра — это радиус основания цилиндра CD и AB.
Образующая цилиндра называется отрезок DB, соединяющий соответственные точки двух окружностей.
Сверху и снизу цилиндр ограничен кругами и называются они основаниями цилиндра.
Осью цилиндра – это прямая, проходящая через центры оснований.
Высота цилиндра и его образующая равны между собой.
1) Основания равны и параллельны.
2) Все образующие цилиндра взаимно параллельны и равны.
3) Все высоты цилиндра взаимно параллельны и равны.
Видео:Видеоурок по математике "Цилиндр"Скачать
wiki.eduVdom.com
Инструменты пользователя
Инструменты сайта
Боковая панель
Стереометрия:
Видео:№528. Докажите, что если секущая плоскость параллельна оси цилиндра и расстояние междуСкачать
Цилиндр
Цилиндром ( прямым круговым цилиндром ) называется тело, состоящее из двух кругов ( оснований цилиндра ), совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие при параллельном переносе точки этих кругов. Отрезки, соединяющие соответствующие точки окружностей оснований, называются образующими цилиндра.
Цилиндр — тело, которое ограничено цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями, пересекающими образующие данной поверхности.
Цилиндрическая поверхность — поверхность, которая образуется движением прямой линии вдоль некоторой кривой. Прямую называют образующей цилиндрической поверхности, а кривую линию — направляющей цилиндрической поверхности.
Боковая поверхность цилиндра — часть цилиндрической поверхности, которая ограничена параллельными плоскостями.
Основания цилиндра — части параллельных плоскостей, отсекаемые боковой поверхностью цилиндра.
Цилиндр называется прямым (См.Рис.1), если его образующие перпендикулярны плоскостям оснований. В противном случае цилиндр называется наклонным.
Круговой цилиндр — цилиндр, основания которого являются кругами.
Прямой круговой цилиндр ( просто цилиндр ) – это тело, полученное при вращении прямоугольника вокруг одной из его сторон. См.Рис.1.
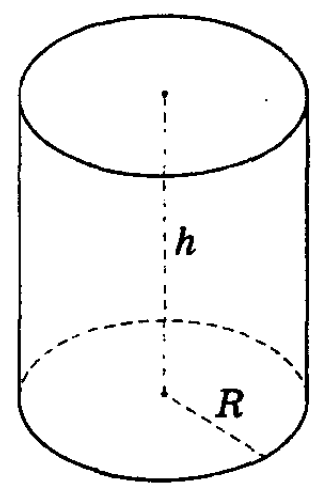
Радиус цилиндра – радиус его основания.
Читайте также: Ремкомплект заднего тормозного цилиндра рено симбол
Образующая цилиндра — образующая цилиндрической поверхности.
Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.
Ось цилиндра параллельна его образующей и является осью симметрии цилиндра.
Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра. См.Рис.2.
Развёртка боковой поверхности цилиндра — прямоугольник со сторонами, равными высоте цилиндра и длине окружности основания.
Площадь боковой поверхности цилиндра — площадь развёртки боковой поверхности. $$S_ =2\pi\cdot rh$$ , где h – высота цилиндра, а r – радиус основания.
Площадь полной поверхности цилиндра — площадь, которая равна сумме площадей двух оснований цилиндра и его боковой поверхности, т.е. выражается формулой: $$S_ =2\pi\cdot r^2 + 2\pi\cdot rh = 2\pi\cdot r(r+h)$$ , где h – высота цилиндра, а r – радиус основания.
Объем всякого цилиндра равен произведению площади основания на высоту: $$V = S\cdot h$$ Объем круглого цилиндра: $$V=\pi r^2 \cdot h$$ , где (r — радиус основания).
Призма есть частный вид цилиндра (образующие параллельны боковым ребрам; направляющая — многоугольник, лежащий в основании). С другой стороны, произвольный цилиндр можно рассматривать как выродившуюся («сглаженную») призму с очень большим числом очень узких граней. Практически цилиндр неотличим от такой призмы. Все свойства призмы сохраняются и в цилиндре.
Видео:№530. Высота цилиндра равна 12 см, а радиус основания равен 10 см. Цилиндр пересеченСкачать
Высотой цилиндра называется расстояние между плоскостями его оснований
11 класс
Материалы к зачетной работе по теме «Тела вращения»
Определение: круговым цилиндром называется тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
Сами круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, — образующими цилиндра.
По свойствам параллельного переноса имеем: основания цилиндра равны и лежат в параллельных плоскостях, а образующие цилиндра параллельны и равны.
Определение: цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.
Радиус оснований цилиндра называется радиусом цилиндра. Расстояние между плоскостями оснований цилиндра называется высотой цилиндра. Прямая, проходящая через центры оснований, называется осью цилиндра. Боковой поверхностью цилиндра называется поверхность, составленная из его образующих.
Теорема: площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра:
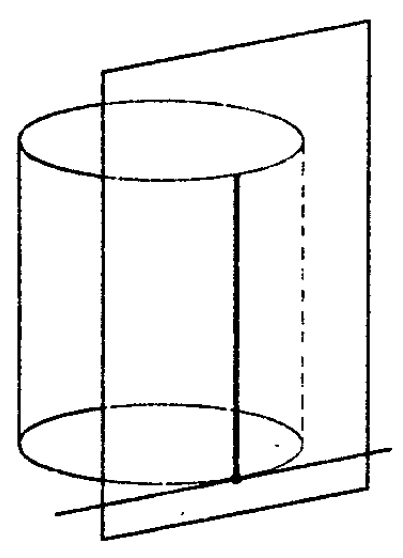
Рассмотрим сечения прямого кругового цилиндра различными плоскостями: осевым сечением называется сечение плоскостью, проходящей через ось цилиндра, оно представляет собой прямоугольник, две стороны которого — образующие цилиндра, а две другие стороны — диаметры оснований цилиндра.
В сечении также может получиться круг, если секущая плоскость перпендикулярна к оси цилиндра.
Примеры:
1. Запаянная с двух концов водосточная труба имеет форму цилиндра.
2. При сечении цилиндра плоскостью, перпендикулярной к оси цилиндра, первоначальный цилиндр распадается на два цилиндра, радиусы которых равны радиусу первоначального цилиндра.
3. Если боковую поверхность прямого кругового цилиндра разрезать по одной из образующих, то в развертке получится прямоугольник.
Определение: тело, которое состоит из круга — основания конуса, точки, не лежащей в плоскости этого круга, — вершины конуса, и всех отрезков, соединяющих вершину конуса с точками основания, называется круговым конусом.
Образующие конуса — отрезки, соединяющие вершину конуса Р с точками окружности основания.
Высота конуса h — перпендикуляр, опущенный из его вершины на плоскость основания. Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, является высотой конуса.
Осью прямого кругового конуса называется прямая, содержащая его высоту.
Боковая поверхность конуса — поверхность, образованная отрезками, соединяющими каждую точку окружности, лежащей в основании конуса, с вершиной конуса.
Теорема: площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.
Примеры:
1. Морковь и сосулька имеют форму, близкую к форме конуса.
2. Если боковую поверхность прямого кругового конуса разрезать по одной из его образующих, то в развертке получится сектор круга, радиус которого равен длине образующей конуса.
3. При вращении прямоугольного треугольника вокруг любого из его катетов получается прямой круговой конус.
Сфера и шар.
Определение: поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки, называется сферой. Центр сферы — данная точка; радиус сферы — данное расстояние; диаметр сферы — отрезок, соединяющий две точки сферы и проходящей через ее центр.
Определение: тело, ограниченное сферой, называется шаром.
Любое сечение шара плоскостью является кругом, а центр этого круга – основание перпендикуляра, опущенного из центра шара на секущую плоскость.
Большим кругом называется сечение шара диаметральной плоскостью — плоскостью, проходящей через центр шара.
Теорема: площадь S сферы радиуса R вычисляется по формуле:
Примеры:
1. Земля и глобус имеют форму, близкую к шару.
2. Если рассмотреть сечение Земли плоскостью, проходящей через экватор, то вся Земля разобьется на два полушария: северное и южное.
3. Баскетбольные, теннисные, футбольные, волейбольные мячи имеют форму шара.
Видео:ЕГЭ Задание 14 Сечение цилиндраСкачать
Опорный конспект по геометрии на тему «Цилиндр»
Ищем педагогов в команду «Инфоурок»
Опр. Цилиндром называется тело, которое состоит из двух кругов, совмещаемых
параллельным переносом и всех отрезков, соединяющих соответствующие точки
Круги называют основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей этих кругов – образующими цилиндра (рис. 1)
1) Основания цилиндра равны и лежат в параллельных плоскостях.
2) Образующие цилиндра равны и параллельны.
Опр. Радиусом цилиндра называется радиус его основания.
Опр. Высотой цилиндра называется расстояние между плоскостями его оснований.
Опр. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.
Осевое сечение цилиндра – прямоугольник со сторонами 2 R и l (в прямом цилиндре l = Н) рис. 2
Сечение цилиндра, параллельные его оси, являются прямоугольниками (рис. 3).
Сечение цилиндра плоскостью, параллельной основаниям – круг, равный основаниям (рис. 4)
Площадь поверхности цилиндра.
Боковая поверхность цилиндра составлена из образующих.
Полная поверхность цилиндра состоит из оснований и боковой поверхности.
S полн = 2 S осн + S бок; S осн = П ∙ R 2 ; S бок = 2 П ∙ R ∙Н S полн = 2П R ∙( R + Н)
№1. Радиус цилиндра равен 3см, а его высота- 5см. Найдите площадь осевого сечения и площадь пол-
№2. Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом и равна 20 см. Найдите площадь боковой поверхности цилиндра.
№3. Радиус цилиндра равен 2см, а его высота- 3см. Найдите диагональ осевого сечения цилиндра.
№4. Диагональ осевого сечения цилиндра, равная , образует с плоскостью основания угол . Найдите площадь боковой поверхности цилиндра.
№5. Площадь боковой поверхности цилиндра равна 15. Найдите площадь осевого сечения.
№6. Найдите высоту цилиндра, если площадь его основания равна 1, а S бок = .
№7. Диагональ осевого сечения цилиндра имеет длину 8см и наклонена к плоскости основания под углом . Найдите полную поверхность цилиндра.
Цилиндрическая дымовая труба с диаметром 65см имеет высоту 18м. Сколько жести нужно для её изготовления, если на заклепку уходит 10% материала?
🎬 Видео
№534. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 120Скачать
Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать
✓ Как решать стереометрию | ЕГЭ-2024. Математика. Профильный уровень. Задание 14 | Борис ТрушинСкачать
Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать
11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать
№527. Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус цилиндра равен г,Скачать
№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать
Объём цилиндраСкачать
№529. Высота цилиндра равна 8 см, радиус равен 5 см. Найдите площадь сечения цилиндраСкачать
РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать
№535. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 60Скачать
Цилиндр и конус имеют общее основание и высоту. Высота цилиндра равна радиусу основания... (ЕГЭ)Скачать
Объем цилиндра.Скачать
№531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельнойСкачать
Длина окружности. Математика 6 класс.Скачать
№537. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длинеСкачать
