Высоту жидкости по объему в горизонтальном цилиндре

Расчет объема жидкости в цилиндрической таре, лежащей на боку (создано по запросу пользователя).

Ага, сегодня я путем несложных умозаключений буду выяснять объем жидкости, находящейся в цилиндрической таре, лежащей на боку.
И это не праздности ради, а дела для.

Цитирую запрос пользователя объем сегмента цилиндра (2):
Доброго времени суток. Видел калькулятор объема сегмента цилиндра, но нужно немножко другое. По работе приходится измерять количество жидкости в таре. Так вот допустим тара цилиндрической формы R=1,13м и H=6,3м лежит на поверхности. Жидкости в таре 0,9м от поверхности. Вопрос: какой объем жидкости в таре?

Там дальше в запросе идут ссылки на решение, но это же не спортивно, поэтому я пошел своим путем ? Сразу замечу, что вторая, более сложная задача — объем жидкости в таре, лежащей под наклоном, еще ждет своего решения.

Вот калькулятор, который все считает, а ход рассуждений, как обычно, под ним.

Объем жидкости в цилиндрической таре

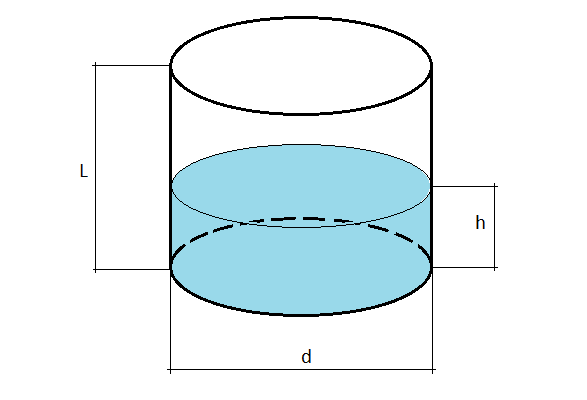
Итак, сформулируем задачу наглядно, и посмотрим на цилиндр в разрезе (см. рисунок). Если уровень жидкости m больше половины, то находим объем воздуха в оставшейся части, а потом вычитаем из общего объема — т. е. всегда сводим к случаю, изображенному на рисунке.

Формула объема всего цилиндра известна — площадь основания, помноженная на высоту.

А нам, значит, надо найти площадь фигуры, залитой синей жидкостью, и тоже помножить на высоту. Пытливый взгляд отметит, что фигура, залитая синей жидкостью, получается из сектора после вычета верхнего треугольника.

Площадь сектора находится как
, где альфа — это угол дуги в радианах.

Угол дуги нам неизвестен. Разберемся сначала с ним. Линия, опущенная вертикально вниз делит верхний треугольник на два прямоугольных треугольника. Гипотенуза у них равна R, а катет, прилежащий к верхнему углу, равен R-m. Таким образом,

и ответ нам Javascript даст как раз в радианах, то что нам нужно.

Теперь разберемся с верхним треугольником. Он равнобедренный, бедра равны R, а основание нам неизвестно. Найдем его.
А оно как раз равно удвоенному противолежащему катету, который, согласно всем известной теореме Пифагора равен

Зная все стороны треугольника, нетрудно найти его площадь по формуле Герона — Расчет площади треугольника по формуле Герона.

Вот, собственно, и все. Мы знаем площадь сектора и площадь треугольника. Вычитаем площадь треугольника из площади сектора, домножаем на высоту цилиндра (или длину цилиндра, с учетом того, что он лежит) и получаем результат.

Видео:Давление. Столб жидкостиСкачать

Расчета объема жидкости в цистерне

Видео:🔴 В сосуде, имеющем форму конуса, уровень жидкости ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Инструкция для калькулятора количества и объема жидкости в цистерне

Размеры вводите в миллиметрах:

D – диаметр емкости можно замерить рулеткой. Необходимо помнить что диаметр – это отрезок наибольшей длины, соединяющий две точки на окружности и проходящий через ее центр.

H – уровень жидкости замеряют, используя метршток, но если такого инструмента нет под рукой, воспользуйтесь обычным стержнем из проволоки или деревянной планкой подходящей длины. Соблюдая меры безопасности, опустите строго вертикально стержень в цистерну до дна, отметьте на нем уровень, достаньте и измерьте рулеткой. Также определить H можно, измерив, расстояние от верха цистерны до поверхности жидкости и отняв этот показатель от значения диаметра.

L – длина емкости.

Если необходим чертеж в бумажном виде, целесообразно отметить пункт «Черно-белый чертеж». Вы получите контрастное изображение и сможете его распечатать, не расходуя зря цветную краску или тонер.

Нажмите «Рассчитать» и получите следующие данные:

Объём емкости – этот параметр характеризует полный объём цистерны, т.е. какое максимальное количество жидкости в кубических метрах или литрах может в нее поместиться.

Читайте также: Главный цилиндр сцепления маз 5440

Количество жидкости – сколько вещества находится в цистерне на данный момент.

Свободный объём позволяет оценить, сколько жидкости еще можно залить в емкость.

В результате, Вы получаете расчет не только объема цистерны, но и объема жидкости в неполной цистерне.

Изделия из металла следует периодически красить, тогда срок их службы значительно возрастет. Зная площадь передней поверхности, площадь боковой поверхности и общую площадь емкости легко оценить необходимое количество лакокрасочных материалов для обработки всей емкости или ее отдельных частей.

Видео:ДАВЛЕНИЕ ЖИДКОСТИ на дно и стенки сосуда 7 класс физика формулаСкачать

Расчет объема жидкости в бочке или цилиндре

Видео:Парадокс сужающейся трубыСкачать

Инструкция для калькулятора расчета объема жидкости в бочке

Впишите размеры неполной вертикальной емкости в миллиметрах:

L – Длина резервуара, т.е. линейный размер цистерны в продольном направлении.

d – Диаметр емкости (численно равен двум радиусам).

Параметры L и d можно измерить рулеткой, лазерным дальномером или линейкой.

h – Высота уровня жидкости, ее определяют мерной линейкой (т.н. метршток), если такого инструмента нет, подойдет обычный стержень из проволоки или дерева подходящей длины. Соблюдая меры безопасности, опустите строго вертикально стержень в емкость до дна, отметив уровень, достаньте и измерьте рулеткой. Также определить h можно, измерив, расстояние от верха цистерны до поверхности жидкости и отняв этот показатель от значения диаметра.

Нажмите «Рассчитать».

Онлайн калькулятор поможет посчитать полный объём емкости и узнать максимальное количество жидкости в кубических метрах или литрах, которое может вместить резервуар. Узнать количество жидкости – сколько вещества поместилось в цистерне. Значение свободного объёма даст представление, сколько жидкости еще влезет в емкость. Также программа вычислит площадь дна, площадь боковой поверхности и общую площадь емкости, что поможет легко прикинуть нужное количество покрасочных материалов для обработки всей цистерны или ее частей.

Видео:Урок 47 (осн). Расчет давления жидкости на дно и стенки сосудаСкачать

Современные способы измерения объема жидкости

Одной из важнейших задач молочной промышленности всегда был учет объема продукта: поступившего на обработку, расходуемого в течение технологического процесса, полученного на выходе. Причем эти измерения требуются как для технологических задач, так и для экономического учета.

О современных способах произведения этих измерений и пойдет речь.Существует несколько подходов к измерению объема жидкости, находящейся в емкости. Все они, однако, имеют одну общую исходную величину, требуемую для расчета. Эта величина – высота столба жидкости.Известна формула, устанавливающая математическую связь между плотностью жидкости, высотой ее столба относительно точки измерения, ускорением свободного падения и давлением, оказываемым на дно и стенки сосуда:

где Р – давление, ρ – плотность жидкости, h – высота столба жидкости, g – ускорение свободного падения (9,8 м/c 2 ).

Итак, зная давление и плотность жидкости, нетрудно рассчитать высоту, до которой она доходит относительно точки измерения. Такой способ измерения называется гидростатическим.Для того, чтобы узнать давление жидкости используются соответствующие датчики. В пищевой промышленности, как правило, это датчики с мембраной, имеющие относительно большую плоскость контакта со средой, что позволяет легко отмывать их от остатков продукта.

Среди датчиков давления наиболее распространены датчики с выходным сигналом 4…20 мА, являющимся общемировым стандартом в системах автоматического управления. Например, интеллектуальный датчик давления 4000-SAN.Сам чувствительный элемент датчика обычно представляет собой тензорезистор – элемент, изменяющий свое сопротивление в зависимости от приложенного к нему усилия. Зависимость сопротивления этих элементов от давления известна. Далее изменение сопротивления электроника датчика приводит к сигналу 4…20 мА.Современные датчики давления часто делаются цифровыми – то есть роль преобразователя играет микроконтроллер, встроенный в датчик. Такие датчики легче настраивать, они обладают более высокой точностью и могут оснащаться дисплеями, модулями коммуникации и дополнительными функциональными возможностями.

Итак, после того, как получено значение высоты, можно переходить к расчету объема жидкости. Выделяются два основных практических подхода:

• геометрическое вычисление;
• аппроксимация линейными отрезками.
  

Видео:Задача про ЦИЛИНДР / Как найти объем детали? / Профиль ЕГЭСкачать

1. Первый способ измерения объема жидкости: вычисление высоты

Первый способ подразумевает возможность выражения зависимости высота – объем известной формулой. Он актуален для емкостей, имеющих несложную форму и построенных из таких стандартных геометрических фигур, как, например, полусфера, конус и цилиндр. Например, для широко распространенных емкостей в форме цилиндра с коническим дном (Рисунок 2), вычисление будет производиться следующим образом: до тех пор, пока жидкость не достигла края конуса зависимость ее объема от высоты такова:

Читайте также: Блок цилиндров ваз 21083 чертеж

Где V – объем, Нж – высота столба жидкости, K – конусность

как только высота жидкости достигает края конуса и начинает заполнять цилиндр достаточно взять заранее вычисленный полный объем конической части:

и прибавлять к нему объем жидкости, находящейся в цилиндрической части:

С учетом степени развития микроконтроллеров, подобный алгоритм возможно реализовать непосредственно в датчике. Не нужно никакое внешнее устройство – датчик сам вычислит объем жидкости, если ввести ее плотность и геометрию емкости.Этот способ, однако, имеет определенные недостатки и ограничения. Они будут рассмотрены далее.

Видео:Гидростатическое давлениеСкачать

2. Точность измерения давления, производимого датчиком

Отдельно нужно отметить требования к точности измерения давления, производимого датчиком. Нетрудно посчитать, что общепромышленный датчик давления, имеющий погрешность в 0,5 % для емкости высотой в 3 метра даст ошибку измерения в:

Значение не кажется столь большим. Однако, если емкость при этом имеет диаметр, скажем, в 2 метра, погрешность вычисления объема составит:

Достаточно большое значение, с учетом того, что в течение рабочего дня могут производиться десятки циклов наполнения/опустошения емкости. При этом данное значение не учитывает дополнительную погрешность, вызываемую перепадами температуры.Именно поэтому датчики для решения задач вычисления объема обычно имеют погрешность не более 0,1 %. При тех же условиях, такой датчик даст ошибку измерения всего в 9,42 литра, то есть в 5 раз меньшую.

Видео:Расчёт давления жидкости на дно и стенки сосуда | Физика 7 класс #30 | ИнфоурокСкачать

3. Второй способ вычисления: аппроксимация

На практике часто встречаются емкости, имеющие искажения формы внутренней поверхности, к которым неприменим геометрический метод вычисления объема емкости.Например, для емкости, установленной под углом (Рисунок 2), наклон в 2…3 градуса, кажущийся незначительным, сильно нарушит точность измерений – в горизонтальной емкости поверхность жидкости вместо прямоугольника будет иметь гораздо более сложную форму, что значительно меняет зависимость объема от уровня.

Емкость может иметь утопленный в стенку люк. В этом случае нужно производить вычисления уже по трем разным формулам, вместо двух. К тому же, зависимость объема на участке с люком будет куда более сложной, чем для прямого цилиндра. Также, геометрический метод на практике неприменим к емкостям, в которых производится перемешивание продукта.

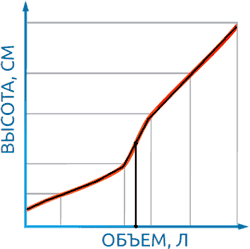
Массивное устройство внутри емкости значительно исказит результаты вычислений – датчик будет показывать объем, больший, чем реальный. Предусмотреть готовые алгоритмы для каждой подобной ситуации и внести их в датчик – задача практически невыполнимая. Тут на помощь приходит более трудоемкий, но и значительно более гибкий способ измерения. Если начать заливать в емкость, допустим, по 100 литров жидкости и при этом на каждом шаге отмечать высоту, соответствующую залитому объему, мы получим так называемую «тарировочную таблицу». Суть в следующем: нестандартная форма емкости моделируется с использованием некоторого количества прямых отрезков. Чем их больше, тем точнее будут производиться вычисления. Таким образом, можно высоте столба жидкости поставить в соответствие ее объем.

Рисунок 3 — Реальная и аппроксимированная зависимости объема жидкости от высоты

Если жидкость, например, находится посередине между двумя точками, то и объем вычисляется, как среднее значение объемов в этих точках (Рисунок 3). Очевидно, что от количества точек, используемых при тарировании, значительно зависит точность результата. Если для участка с линейной зависимостью объем/высота достаточно двух точек, до для нелинейных участков их требуется гораздо больше. Тарирование на нелинейном участке можно производить шагами, в два раза большими, чем допустимая погрешность на данном участке. Например, если в конусной части емкости необходимо получить точность не ниже 20 литров, шаги тарирования должны быть не более 40 литров. Тут следует помнить простое правило – чем меньше шаги и больше точек, тем выше итоговая точность работы. Недостаток метода в том, что датчик, перенесенный на другую емкость, снова потребует тарирования. Однако, единожды оттарированный на одной емкости датчик будет не только давать максимально высокую точность вычислений, но и позволит подсчитывать объем для жидкостей с различными плотностями – достаточно будет лишь ввести в него это значение.

Это значит, что можно произвести тарирование с использованием обычной воды, а затем, предварительно поменяв значение плотности жидкости в памяти датчика, заливать продукт, имеющий плотность, отличную от плотности воды. Таким образом, мы получаем гибкий и точный метод, позволяющий работать с емкостями любой формы и жидкостями любой плотности.

Читайте также: Хендай акцент пропуски зажигания во всех цилиндрах

Инженер отдела проектирования ООО «КИП-Сервис»
Горбоносов М.А.

Видео:Урок 46 (осн). Передача давления жидкостями и газами. Закон ПаскаляСкачать

Калькулятор расчета жидкости в бочке, цистерне, цилиндре

Инструкция для калькулятора расчета физических показателей круглой емкости

При помощи онлайн калькулятора Вы сможете правильно рассчитать объем емкости типа: цилиндра, бочки, цистерны или объем жидкости в любой другой горизонтальной цилиндрической емкости.

Определим количество жидкости в неполном баке цилиндрической формы

Все параметры указываем в миллиметрах

L — Высота бочки.

H — Уровень жидкости.

D — Диаметр бака.

Наша программа в онлайн режиме выполнит расчет количества жидкости в емкости, определит площадь поверхностей, свободную и общую кубатуру.

Как посчитать объем бочки

Для тог, чтобы правильно рассчитать вместительность резервуара для определения количества жидкости и полезной кубатуры цилиндрической емкости, необходимо определить основные параметры бака. В нашем случае это горизонтальная цистерна.

Определение главных параметров кубатуры резервуаров (к примеру, обычная бочка или цистерна) должен производиться, основываясь на геометрическом методе расчета вместительности цилиндров. В отличие от способов калибровки емкости, где подсчет объема выполняют в виде реальных измерений количества жидкости путем мерной линейки (согласно показаниям метрштока).

V=S*L – формула расчета объема бака цилиндрической формы, где:

S — площадь поперечного сечения резервуара.

Согласно полученным результатам создают калибровочные таблицы емкости, которые еще называются тарировочными, позволяют определить вес жидкости в баке по удельному весу и объему. Эти параметры будут зависеть от уровня наполнения цистерны, который можно измерять при помощи метрштока.

Наш онлайн калькулятор предоставляет возможность выполнить расчет вместительности горизонтальных и вертикальных емкостей по геометрической формуле. Вы сможете узнать полезную вместительность резервуара более точно, если при этом правильно определите все главные параметры, которые указаны выше и участвуют в расчете.

Как правильно определить основные данные

Определяем длину L

При помощи обычной рулетки, Вы сможете измерить длину L цилиндрического резервуара с неплоским дном. Для этого Вам необходимо замерить расстояние между пересекающими линиями днища с цилиндрическим телом емкости. В случае, когда горизонтальный бак с плоским дном, то для того, чтобы определить размер L, достаточно измерить длину резервуара по наружной стороне (от одного края бака до другого), и от полученного результата вычесть толщину дна.

Определяем диаметр D

Проще всего определить диаметр D бочки цилиндрической формы. Для этого достаточно при помощи рулетки замерять расстояние между двумя любыми крайними точками крышки или края.

Если трудно правильно выполнить расчет диаметра емкости, то в этом случае можно использовать измерение длины окружности. Для этого при помощи обычной рулетки обхватываем по окружности весь резервуар. Для правильно расчета окружности делают два измерения в каждом сечении резервуара. Для этого поверхность, измеряемая должна быть чистой. Узнав усредненную длину окружности нашей емкости – Lокр, переходим к определению диаметра по следующей формуле:

Этот метод наиболее простой, так как зачастую измерение диаметра бака сопровождается рядом затруднений, связанных с нагромождением на поверхности различного вида оборудования.

Важно! Измерения диаметра правильней всего выполнить в трех разных сечениях емкости, и после этого выполнить подсчет среднего значения. Так как зачастую, эти данные могут существенно отличаться.

Усредненные значения после трех замеров позволяют минимизировать погрешность расчета объема резервуара цилиндрической формы. Как правило, используемые накопительные баки во время эксплуатации подвергаются деформации, могут терять прочность, уменьшаться в размерах, что ведет к уменьшению количества жидкости внутри.

Определяем уровень H

Чтобы определить уровень жидкости, в нашем случае это H, нам понадобиться метршток. При помощи этого измерительного элемента, который опускают на дно емкости, мы сможем точно определить параметр H. Но эти расчеты будут верны для резервуаров с плоским дном.

В результате подсчета онлайн калькулятора мы получаем:

• Свободный объем в литрах;
• Количество жидкости в литрах;
• Объем жидкости в литрах;
• Общую площадь резервуара в м²;
• Площадь дна в м²;
• Площадь боковой поверхности в м².

💥 Видео

Физика 7 класс (Урок№20 - Расчёт давления жидкости на дно и стенки сосуда.)Скачать

Зависимость давления в жидкости от глубины погруженияСкачать

Как высчитать обьем воды в трубе ( Формула )Скачать

В горизонтальном цилиндрическом сосуде - Задача ЕГЭ по физике Часть 2Скачать

Закон БернуллиСкачать

Что такое давление? Как его создать? Абсолютное и избыточное давлениеСкачать

На горизонтальном столе стоит пустой цилиндрический сосуд высотой 1 м с площадью дна 100 см2- №23061Скачать

🔴 В сосуде, имеющем форму конуса, уровень жидкости ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Объём цилиндраСкачать

Урок 59 (осн). Жидкостный поршневой насосСкачать

Как поднимали воду до Нашей Эры? Акведук и давление столба жидкости в физике.Скачать