Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.
- Объем правильного цилиндра через радиус и высоту цилиндра
- Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра
- Формулы и калькулятор для вычисления объема цилиндра через диаметр основания
- Объем цилиндрической полости
- Поверхности цилиндра
- Сечения цилиндра
- Что такое объем
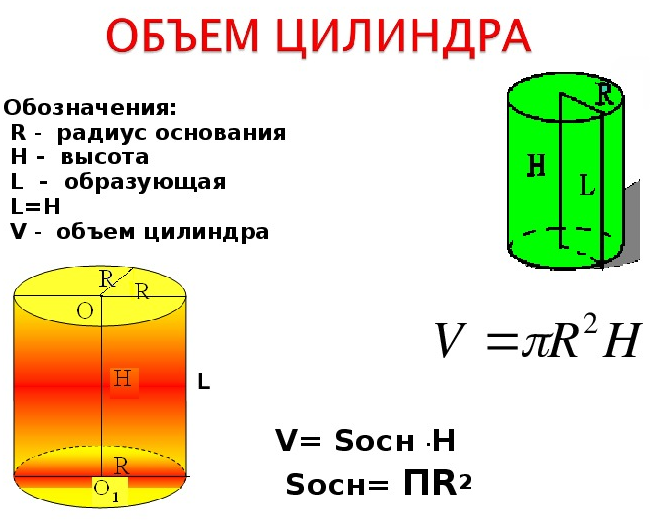
- Формула объема цилиндра
- Объем прямого цилиндра
- Объем цилиндра через радиус основания и высоту цилиндра
- Объем цилиндра через площадь основания и высоту цилиндра
- Объем цилиндра через диаметр основания и высоту цилиндра
- Нахождение объема цилиндра: формула и задачи
- Формула вычисления объема цилиндра
- Через площадь основания и высоту
- Через радиус основания и высоту
- Через диаметр основания и высоту
- Примеры задач
- Папка-кейс на тему: «Объём цилиндра» методическая разработка по геометрии (11 класс) на тему
- Скачать:
- Предварительный просмотр:
- 💡 Видео
Видео:11 класс, 32 урок, Объем цилиндраСкачать

Объем правильного цилиндра через радиус и высоту цилиндра
Видео:Как вывести формулу для вычисления объёма прямого кругового конуса без интегрирования?Скачать

Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра
Видео:Цилиндр - расчёт площади, объёма.Скачать

Формулы и калькулятор для вычисления объема цилиндра через диаметр основания
Видео:11 класс. Геометрия. Объем цилиндраСкачать

Объем цилиндрической полости
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.
Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.
Рассмотрим правильный цилиндр.
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.
Радиус основания цилиндра, является радиусом цилиндра.
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

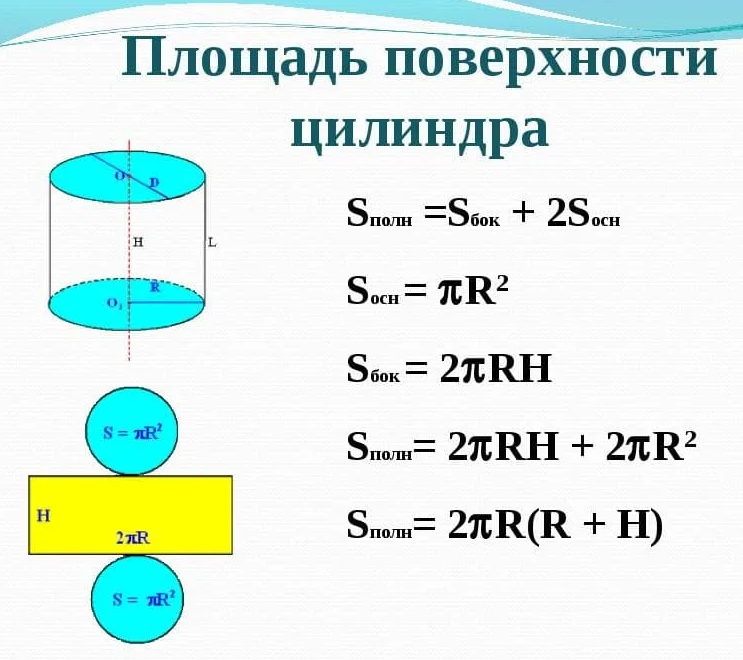
Поверхности цилиндра
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).
Видео:Видеоурок по математике "Цилиндр"Скачать

Сечения цилиндра
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура .
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник , но две боковые стороны которого будут являться кривыми линиями.
Читайте также: Чери амулет а15 задний тормозной цилиндр артикул
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг .
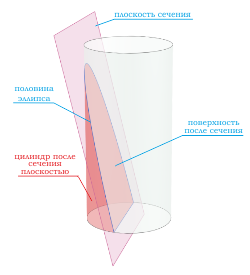
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс .
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса .
Видео:Как вывести формулу для вычисления объём шара без использования интегрирования?Скачать

Что такое объем
Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм 3 , см 3 , мл 3 .
Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.
Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.
Объем и площадь других видов цилиндров рассмотрен в статьях:
Видео:Объём цилиндраСкачать

Формула объема цилиндра
Цилиндр – это геометрическое тело, которое имеет цилиндрическую поверхность, называемое еще как боковая поверхность цилиндра и имеет две поверхности, которые носят название оснований цилиндра. Круговым цилиндр называют, если у него в основании лежит круг.
Высота цилиндра — это отрезок, соединяющий две любые точки оснований но обязательно расположенный перпендикулярно к ним обоим.
Видео:Как найти объем. Принцип Кавальери | Ботай со мной #050 | Борис Трушин |Скачать

Объем прямого цилиндра
Цилиндр — это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. Слово «цилиндр» происходит от греческого слова «kylindros».
Объем цилиндра через радиус основания и высоту цилиндра
Объем цилиндра равен произведению квадрата радиуса основания, высоты цилиндра и числа пи (3.1415)
\[ \LARGE V = \pi \cdot R^ \cdot H \]
где:
V — объем цилиндра
π — число пи (3.1415)
R — радиус основания
H — высота цилиндра
Объем цилиндра через площадь основания и высоту цилиндра
Объем цилиндра равен произведению площади основания цилиндра на его высоту.
где:
V — объем цилиндра
H — высота цилиндра
S — площадь цилиндра
Объем цилиндра через диаметр основания и высоту цилиндра
Объем цилиндра равен произведению диаметра основания и числа пи (3.1415) делённое на четыре высоты цилиндра
где:
V — объем цилиндра
π — число пи (3.1415)
D — диаметр основания
H — высота цилиндра
Видео:Объем цилиндра. Практическая часть. 11 класс.Скачать

Нахождение объема цилиндра: формула и задачи
В данной публикации мы рассмотрим, как можно найти объем цилиндра и разберем примеры решения задач.
Видео:11 класс, 37 урок, Объем шараСкачать

Формула вычисления объема цилиндра
Через площадь основания и высоту
Объем (V) цилиндра равняется произведению его высоты и площади основания.
Через радиус основания и высоту
Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R 2 . Следовательно, формулу для вычисления объема цилиндра можно представить в виде:
V = π ⋅ R 2 ⋅ H
Примечание: в расчетах значение числа π округляется до 3,14.
Через диаметр основания и высоту
Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:
Видео:11 класс, 36 урок, Объем конусаСкачать

Примеры задач
Задание 1
Найдите объем цилиндра, если дана площадь его основания – 78,5 см 2 , а также, высота – 10 см.
Читайте также: Как выкрутить сломанный штуцер прокачки тормозов заднего цилиндра
Решение:
Применим первую формулу, подставив в нее известные значения:
V = 78,5 см 2 ⋅ 10 см = 785 см 3 .
Задание 2
Высота цилиндра равна 6 см, а его диаметр – 8 см. Найдите объем фигуры.
Решение:
Воспользовавшись третьей формулой, в которой участвует диаметр, получаем:
V = 3,14 ⋅ (8/2 см) 2 ⋅ 6 см = 301,44 см 3 .
Видео:Архимед и объём шараСкачать

Папка-кейс на тему: «Объём цилиндра»
методическая разработка по геометрии (11 класс) на тему
В папке – кейс содержатся следующие материалы
- Задание № 1. Выведите формулу для нахождения объема цилиндра, используя формулу Симпсона.
- Задание № 2. Решите задачи ЕГЭ на вычисление объема цилиндра.
- Задание № 3. Задание для участников других групп.
- Задание № 4. Решите задачи по своей теме практического содержания.
- Задание № 5. Приготовьте защиту проекта: интересное о цилиндрах и решение задач практического содержания.
Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Скачать:
Как сдать ЕГЭ на 80+ баллов?
Репетиторы Учи.Дома помогут подготовиться к ЕГЭ. Приходите на бесплатный пробный урок, на котором репетиторы определят ваш уровень подготовки и составят индивидуальный план обучения.
Бесплатно, онлайн, 40 минут
Видео:Интегралы №13 Объем тела вращенияСкачать

Предварительный просмотр:
В папке – кейс содержатся следующие материалы
- Задание № 1. Выведите формулу для нахождения объема цилиндра, используя формулу Симпсона.
- Задание № 2 . Решите задачи ЕГЭ на вычисление объема цилиндра.
- Задание № 3. Задание для участников других групп.
- Задание № 4. Решите задачи по своей теме практического содержания.
- Задание № 5. Приготовьте защиту проекта: интересное о цилиндрах и решение задач практического содержания.
Выведите формулу для нахождения объема цилиндра, используя формулу Симпсона.
где — предельные значения высоты геометрического тела,
– площадь нижнего основания,
— площадь среднего сечения ( сечение тела плоскостью, параллельной основанию, и проходящей через середину высоты ),
— площадь верхнего основания.
Выполните следующие задания.
Задача № 1. В цилиндрический сосуд налили
2000 см 3 воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объём детали. Ответ выразите в см 3 .
Задача № 2. Дано два цилиндра. Объём первого цилиндра равен 12. У второго цилиндра высота в 3 раза больше, а радиус основания в 2 раза меньше, чем у первого. Найдите объём второго цилиндра.
Задача № 3. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объёма второй кружки к объёму первой.
Придумайте или найдите задачи на нахождения объема цилиндра, задачи с использованием формулы объема цилиндра для учащихся других групп (Из различных источников).
Найдите задачи, решите их самостоятельно, оформите их для представления учащимся других групп и затем будьте экспертами при решении ими задач (каждой группе по 1 задаче)
Задачи практического содержания
Задача № 1. Поднятие «Садко»-(наибольший ледокол, затонувший в 1969 году).
« Садко» — ледокольный пароход, внесший значительный вклад в освоение Арктики и Северного морского пути. Назван в честь былинного героя Садко . 11 сентября 1941 года , на пути из Диксона на Землю Франца-Иосифа , «Садко» наскочил на ранее неизвестную подводную банку вблизи островов Известий ЦИК в Карском море и затонул. Погиб один человек, остальной экипаж спасен ледоколом « Ленин ».
Так и лежал спокойно пароход «Садко» на глубине в 21 метр с пятиметровой пробоиной по левому борту, пока северная партия ЭПРОНа не решилась поднять судно с помощью двенадцати понтонов.
Читайте также: Что такое кукольный цилиндр
Основные работы начались 15 июня 1932 года. Под «Садко» прорыли с помощью водяных струй 12 тоннелей, завели туда тросы (двойные судоподъемные полотенца).
Каждый цилиндрический понтон (грузоподъемность 200 тонн) имел длину в 11 метров, а диаметр — 5,5 м. Каков объём понтона?
Задача № 2. Сколько тонн нефти может перевезти поезд, имеющий в своём составе 15 цистерн, если диаметр котла каждой 3м, а длина 10,8 м, а плотность нефти составляет 850 кг/м 3 ?
Некоторые важные моменты транспортировки
Перед наливом нефти в резервуар для перевозки, этот резервуар должен быть специальным образом подготовлен, а именно, очищен от ранее перевозимого вещества. Резервуар должен иметь маслобензостойкое, паростойкое покрытие с электростатической безопасностью. Категорически запрещается перевозить нефть в резервуарах, в которых раньше перевозились бензин, керосин и другие горючие вещества.
Цилиндры Фараона — два загадочных предмета цилиндрической формы в руках некоторых древнеегипетских изваяний. Среди специалистов-египтологов не существует единого мнения о происхождении данных предметов.
В 1976 году в Закавказье Р.Добровольским и В.Ковтуном была обнаружена старинная эзотерическая рукопись под названием «Тайны Жизни и Смерти», в которой содержалась информация о Лунном и Солнечном цилиндрах, изготовленных из цинка и меди с определенным внутренним наполнением.
По утверждению неизвестного автора Цилиндры Фараона использовались фараонами и жрецами Древнего Египта для укрепления жизненных сил и общения с богами.
Цилиндры Фараона были воссозданы согласно древнему рецепту и затем в течение многих лет исследовались физиком Владимиром Ковтуном. В этих исследованиях принимали участие медики, физики, египтологи, экстрасенсы и парапсихологи. Результаты исследований поразили ученых.
Оказалось, что Цилиндры Фараона обладают широчайшим спектром благотворного воздействия на организм человека. В него входят: помощь при сердечно-сосудистых заболеваниях, нейротрофических, гипертонии, болезнях выводящих путей, астме, бессоннице, головных болях а также в качестве средства для снятия стрессов и профилактике атеросклероза.
Одна из удивительных особенностей Цилиндров Фараона — улучшение работы практически всех основных систем организма (показатели работы этих систем улучшаются в среднем в 2 — 2.5 раза)
Согласно мнению ряда врачей Цилиндры Фараона представляют собой уникальный, самонастраивающийся на каждого человека, физиотерапевтический прибор, созданный гением древнеегипетских ученых. Их целебные свойства, включающие в себя металлотерапию, гальванотерапию и магнитотерапию позволили врачу-биоэнергетику Т.Мешковой разработать эффективную методику использования Цилиндров. Цилиндры Фараона полезны как взрослым людям так и детям. Они создают в организме человека обстановку, при которой ему гораздо легче справляться со своими бедами. Цилиндры — прекраснее профилактическое средство против ряда болезней.
В XVIII веке цилиндр стал мужским головным убором. Новый головной убор в виде «трубы» на голове шляпного торговца Джона Гетерингтона стал для чопорных англичан сенсацией. Тогдашние газеты писали: «Действие шляпы на прохожих было ужасным. Многие женщины при виде этого странного предмета лишались чувства, дети кричали. »
А сам Гетерингтон был арестован и доставлен к лорду-мэру, который за нарушение общественного порядка приговорил его к штрафу в 500 фунтов стерлингов. Тем не менее эта прогулка по лондонской набережной 26 января 1797 года стала датой рождения нового направления моды. В начале XIX века цилиндр был исключительно аристократической принадлежностью.
Цилиндры применялись в архитектуре с древнейших времен. Например, колонны чаще всего имели цилиндрическую форму.
И сегодня цилиндр – главный помощник архитектора в его работе.
💡 Видео
Объем цилиндраСкачать

11 класс, 38 урок, Объемы шарового сегмента, шарового слоя и шарового сектораСкачать

Объем цилиндра.Скачать

Вывод формулы объёма пирамидыСкачать

Стереометрия на ЕГЭ по математике. Вычисление объема части цилиндра.Скачать