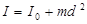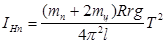Вывести формулу для относительной погрешности измерения момента инерции цилиндра (5 видео)

Содержание

Определение относительной погрешности при вычислении момента инерции цилиндра
Момент инерции цилиндра сплошного и полого: разное положение осей вращения
Момент инерции: математическое определение
Момент инерции цилиндра относительно оси, его основаниям перпендикулярной
Момент инерции полого цилиндра
Величина I для цилиндра, ось вращения которого проходит параллельно плоскостям его основания
Пример решения задачи
Вывести формулу для относительной погрешности измерения момента инерции J цилиндра (J=1/2mR^2)
Вывести формулу для относительной погрешности измерения момента инерции J цилиндра (J=1/2mR^2) — Физика — Ответ 14916696
Лабораторная работа: Определение момента инерции твердых тел 3
💡 Видео

Видео:Расчёт момента инерции тела относительно оси вращения. Момент инерции однородного стержняСкачать

Определение относительной погрешности при вычислении момента инерции цилиндра

Определение момента инерции цилиндра, если ось вращения проходит через центр масс (используются 2 цилиндра)

Проверка теоремы Штейнера

При переносе оси вращения или отдельных частей тела относительно этой оси его момент инерции изменяется. Соотношение между моментами инерции тела относительно некоторой оси вращения, проходящей через центр масс, и относительно произвольной, параллельной ей оси устанавливается с помощью теоремы Гюйгенса- Штейнера.

Рабочая формула:

m_n – масса платформы (228 грамм)

R – радиус платформы (10 см)

m_ц – масса 1 цилиндра (745 гр)

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Видео:Расчет момента инерции цилиндраСкачать

Момент инерции цилиндра сплошного и полого: разное положение осей вращения

Знание момента инерции тела позволяет воспользоваться законом сохранения момента импульса либо выражением для описания кругового движения с угловым ускорением. В данной статье рассмотрим, как находить для цилиндра момент инерции при различном положении осей вращения.

Видео:Урок 94. Вычисление моментов инерции телСкачать

Момент инерции: математическое определение

Осевой момент инерции вводится в физику благодаря изучению законов вращательного движения тел. Для точки материальной с массой m, вращающейся на расстоянии r от оси, момент инерции будет равен:

В общем же случае для тела, которое имеет произвольное распределение вещества в пространстве (любую геометрическую форму), величину I можно вычислить так:

По сути, это выражение является обобщением предыдущего. В нем производится суммирование (интегрирование) моментов от каждой элементарной частицы dm, дистанция до оси от которой равна r.

Если говорить о физическом значении рассматриваемой величины I, то она показывает, насколько «сильно» система сопротивляется воздействию внешнего момента силы, который пытается ее раскрутить или, наоборот, остановить.

Видео:Расчет момента инерции диска или цельного цилиндраСкачать

Момент инерции цилиндра относительно оси, его основаниям перпендикулярной

Из приведенной выше формулы можно понять, что величина I является характеристикой всей вращающейся системы, то есть она зависит как от формы тела и распределения в нем массы, так и от относительного положения оси.

В данном пункте рассмотрим простой случай: определить необходимо момент инерции для сплошного цилиндра, ось вращения которого перпендикулярна его основаниям и проходит через гравитационный центр фигуры.

Для решения проблемы применим интегральную формулу для I. В процессе операции интегрирования мысленно разобьем цилиндр на тонкие колечки толщиной dr. Каждое колечко будет иметь объем: dV = 2*pi*r*dr*h, здесь h — высота фигуры. Учитывая, что dm = ρ*dV, где ρ — плотность цилиндра, получаем:

I = ∫r 2 dm = ρ*∫r 2 dV = 2*pi*ρ*h*∫r 3 dr

Этот интеграл необходимо вычислить для пределов от 0 до R, где R — радиус фигуры. Тогда получим:

I = 2*pi*ρ*h*∫ R ₀r 3 dr = 2*pi*ρ*h/4*(r 4 )∣ R ₀ = pi*ρ*h*R 4 /2

Воспользовавшись формулой для массы цилиндра через его объем и плотность, приходим к конечному выражению:

Мы получили формулу инерции момента цилиндра однородного. Она показывает, что величина I для этой фигуры в 2 раза меньше, чем для материальной точки аналогичной массы, которая вращается на расстоянии радиуса цилиндра от оси.

Видео:момент инерции цилиндраСкачать

Момент инерции полого цилиндра

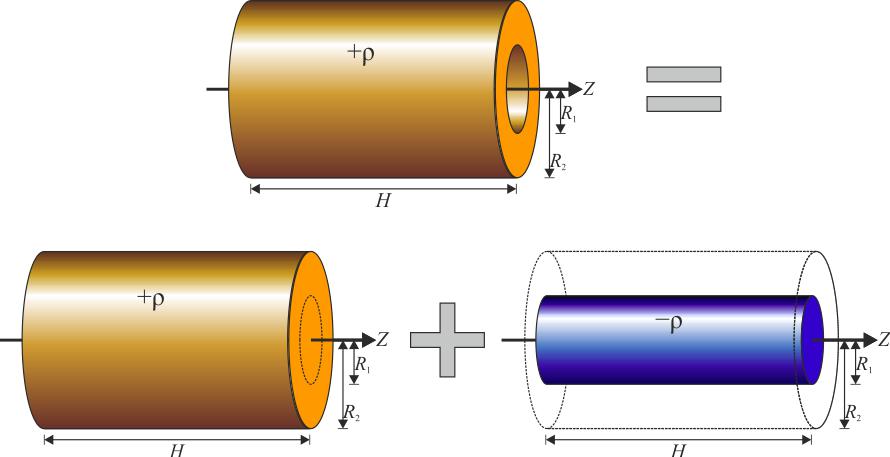
Теперь оставим ось на том же месте и найдем значение I для цилиндра с пустотой внутри (втулка, труба). Такую фигуру описывают двумя радиусами: внешним R₁ и внутренним R₂. В этом случае для интегрирования применяется абсолютно тот же подход, что и для сплошного цилиндра, только пределы теперь изменяются от R₂ до R₁. Имеем:

Для дальнейшего упрощения этой формулы воспользуемся разложением на множители выражения в скобках, получим:

Часть этого выражения вместе с первыми скобками является массой полого цилиндра, поэтому получаем конечную формулу:

Отсюда видно, что момент инерции полого цилиндра больше этого значения для сплошного цилиндра аналогичной массы и такого же внешнего радиуса на величину m*R₂ 2 /2. Этот результат не вызывает удивления, поскольку в полом цилиндре центр масс находится от оси вращения дальше, чем в сплошном.

Видео:Момент инерцииСкачать

Величина I для цилиндра, ось вращения которого проходит параллельно плоскостям его основания

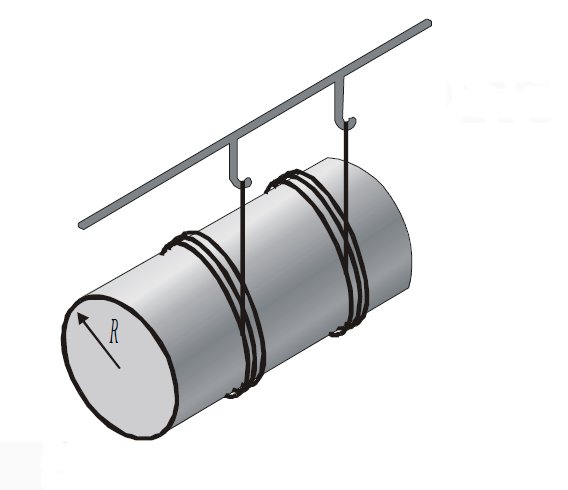
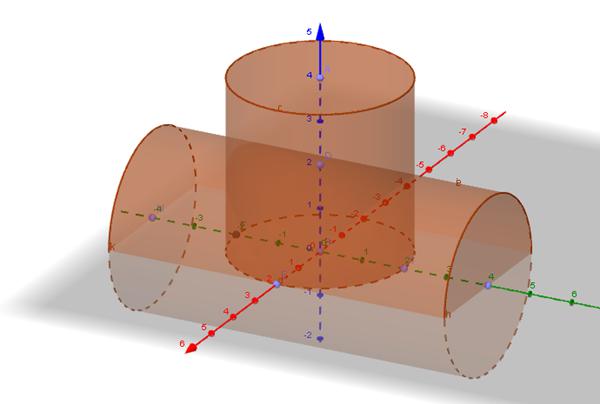
В такой системе ось вращения проходит также через центр массы цилиндра, но теперь он лежит как бы на боку (на цилиндрической поверхности, см. рис. ниже).

Расчет для момента инерции цилиндра для такой ситуации является непростой задачей, поскольку требует наличия дополнительных знаний для ее решения. Тем не менее приведем необходимые математические выкладки, чтобы читатели имели более полное представление о проведении интегрирования при вычислении I.

Читайте также: Площадь цилиндра с разными основаниями формула

Начинаем решать задачу. Разбиваем сплошной цилиндр на отдельные диски бесконечно малой толщины. Чтобы узнать, каким моментом инерции обладает этот диск относительно оси, которая проходит через него и параллельна его основаниям, необходимо выполнить отдельное интегрирование. Оно дает следующий результат:

Чтобы найти, величину I_i для этого диска относительно уже новой оси, которая рассматривается в задаче, необходимо воспользоваться теоремой Штейнера. Получим:

I_i = R 2 *dm/4 + L 2 *dm, здесь L — расстояние от оси до тонкого диска.

Зная, что dm = pi*R 2 *dL*ρ, подставляем в интегральную формулу для I и проводим интегрирование по пределам (-L₀/2; +L₀/2), имеем:

I = ∫_mI_i = ∫_m(R 2 *dm/4 + L 2 *dm) = pi*R 2 *ρ*∫ L0/2 _-L0/2(R 2 *dL/4 + L 2 *dL)

Решение этого интеграла приводит к конечной формуле:

Видео:Относительная и абсолютная погрешностьСкачать

Пример решения задачи

Решим интересную задачу на нахождение осевого момента инерции цилиндра. Пусть он лежит на цилиндрической поверхности, а ось вращения расположена параллельно его основанию и проходит через конец фигуры.

Эта ситуация полностью аналогична рассмотренной в предыдущем пункте, только ось пересекает не гравитационный центр цилиндра, а конец этой фигуры. Тем не менее для решения проблемы можно воспользоваться результатом предыдущего пункта статьи. Применим вышеупомянутую теорему Штейнера, получим:

I = m*R 2 /4 + m*L₀ 2 /12 + m*(L₀/2) 2 = m*R 2 /4 + m*L₀ 2 /3

Этот момент инерции соответствует стержню с осью вращения на его конце.

Видео:Расчет момента инерции тонкого стержняСкачать

Вывести формулу для относительной погрешности измерения момента инерции J цилиндра (J=1/2mR^2)

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Как вывести формулу для относительной погрешности
Если есть вот такое выражение Y = X12*X23/12 ,как для него можно вывести формулу относительной.

Вывести формулу для момента инерции прямого кругового конуса
Вывести формулу для момента инерции прямого кругового конуса относительно его высоты, М — масса.

15. Напишите формулу для оценки погрешности косвенного измерения величины Z = 7Y3(3X + 5)2, если ΔX и ΔY известны
Напишите формулу для оценки погрешности косвенного измерения величины Z = 7Y3(3X + 5)2, если.

Составьте программу для вычисления момента инерции
задача по информаике составьте программу для вычисления момента инерции, момента сопротивления.

Формула для расчета момента инерции барабана с проволокой
Необходима формула для расчета момента инерции барабана со сварочной проволокой, соответственно для.

Формула относительной погрешности
Уважаемые физики, пожалуйста помогите! Делаю лабораторную работу и там один из контрольных вопросов.

Вычисление относительной погрешности полинома
Относительная погрешность ведь не может быть отрицательной. А что делать если один из коэффициентов.

Вычисление абсолютной и относительной погрешности
Помогите пожалуйста, нужно написать програму которая будет считать абсолютную и относительную.

Вывод формул абсолютной и относительной погрешности частного
Нужно вывести формулы для абсолютной и относительной погрешности частного. Вот что у меня.

Видео:Урок 98. Задачи на вычисление моментов инерции (ч.1)Скачать

Вывести формулу для относительной погрешности измерения момента инерции J цилиндра (J=1/2mR^2) — Физика — Ответ 14916696

Если Вам известна формула для вычисления относительной погрешности величины, которая является функцией нескольких независимых переменных, то воспользуйтесь ею. Если эта формула Вам неизвестна, то поищите её в используемом Вами учебнике или в конспекте лекций, или в другом источнике, который рекомендован обучающей Вас кафедрой. В частности, нужные Вам сведения есть в книге «Курс физики», написанной А. А. Детлафом и Б. М. Яворским.

Читайте также: Цилиндр отрыва борта для шиномонтажного станка 1885it trommelberg

Видео:Урок 97. Теорема ШтейнераСкачать

Лабораторная работа: Определение момента инерции твердых тел 3

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Лабораторная работа по курсу «Общая физика»

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДЫХ ТЕЛ

Преподаватель Студент группы

___________ / ____________ / __________/

___________2009 г. ____________ 2009 г.

Целью настоящей работы является определение момента инерции твердых тел и экспериментальная проверка справедливости теоремы Штейнера на примере физического маятника.

2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА

Для экспериментальной проверки теоремы Штейнера и определения момента инерции в данной работе используется стандартная установка универсального маятника ФПМО — 4. Это настольный прибор (рис. 4.1), на вертикальной стойке основания 1 которого крепится кронштейн 2, который имеет возможность поворота вокруг стойки на 360° и фиксация в любом выбранном положении. С одной стороны кронштейна 2 подвешен математический маятник, а с другой — физический. Математический маятник представляет собой металлический шарик 3 на бифилярном подвесе 4. Физический маятник — стальной стержень 5, подвешенный на опорной призме 6. Опорная призма 6 может перемещаться по всей длине стержня и фиксироваться в требуемом положении.

Стержень 5 имеет кольцевые проточки, которые служат для надежной фиксации опорных призм. Установка снабжена фотоэлектрическим датчиком 7, который закреплен на вертикальной стойке с помощью кронштейна 8 и имеет возможность перемещаться как вдоль, так и вокруг стойки и фиксироваться в любом положении. Датчик предназначен для выдачи сигналов на миллисекундомер 9. Миллисекундомер физический выполнен самостоятельным прибором с цифровой индикацией времени и количества полных периодов колебаний маятника.

3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ

Средняя величина периода колебаний маятника:

где t — продолжительность 10 — 15 колебаний;

n — число колебаний за время t .

Формула для экспериментального расчета момента инерции прямого тонкого стержня

где T — период колебаний маятника;

l — расстояние от центра масс до точки подвеса маятника;

g — ускорение свободного падения.

Формула для теоретического расчета момента инерции прямого тонкого стержня длиной d и массой m относительно оси, перпендикулярной к стержню и проходящей через его середину:

Формула для теоретического расчета инерции прямого тонкого стержня длиной d и массой mотносительно произвольной оси, параллельной другой оси, перпендикулярной к стержню и проходящей через его середину:

Формула для расчета погрешности косвенного измерения квадрата расстояния между осями:

где s ( l ) – абсолютная погрешность измерения между осями.

Формула для расчета экспериментальной абсолютной погрешности косвенного измерения периода колебания стержня:

Формула для расчета экспериментальной абсолютной погрешности косвенного измерения момента инерции:

где σ ( m ) – абсолютная погрешность измерения массы стержня;

σ ( g ) – абсолютная погрешность измерения ускорения свободного падения;

σ ( π ) – абсолютная погрешность измерения числа π.

4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ.

Результаты прямых и косвенных измерений представлены в таблице.

Номер опыта	n	t , c	T , c	l 2 , м 2	I, кг×м 2	Примечание
1	10	12,777	1,2777	0,0841	0,04313
2	10	12,410	1,2410	0,0625	0,03489
3	10	12,156	1,2156	0,0441	0,02837
4	10	12,094	1,2094	0,0289	0,02259
5	10	12,404	1,2404	0,0169	0,01814
6	10	13,471	1,3471	0,0081	0,01489
7	10	16,719	1,6719	0,0025	0,01265

Подсчитаем среднюю величину периода колебаний маятника (3.1)

T₂ =12,410/ 10 = 1, 2410 с
T₃ =12,156 / 10 = 1, 2156 с
T₄ =12,094 / 10 = 1, 2094 с
T₅ =12,404 / 10 = 1,2404 с
T₆ =13,471 / 10 = 1,3471 с
T₇ =16,719 / 10 = 1,6719 с

Теперь найдем момент инерции прямого тонкого стержня по формуле (3.2)

I₁ = ≈ 0,04313 кг*м 2

I₃ = ≈ 0,02837 кг*м 2

I₇ = ≈ 0,01265 кг*м 2

Абсолютная погрешность замера времени колебаний составляет ± 2 мс, а с учётом вычисления периода ± 2×10 -4 , то вычисляем результаты с точностью до пяти знаков.

Расчёт случайной погрешности измерения для построения графика

t₁ = σ (t) = 12,777 0,02с

t₂ = σ (t) = 12,410 0,02с

t₃ = σ (t) = 12,156 0,02с

t₄ = σ (t) = 12,094 0,02с

t₅ = σ (t) = 12,404 0,02с

t₆ = σ (t) = 13,471 0,02с

t₇ = σ (t) = 16,719 0,02с

От абсолютной погрешности замера времени колебаний зависит момент инерции прямого тонкого стержня, а расстояние от масс до точки подвеса маятника не зависит.

T₁ = σ (t) / n = 1,27770,002с

T₂ = σ (t) / n = 1,24100,002с

T₃ = σ (t) / n = 1,21560,002с

T₄ = σ (t) / n = 1,20940,002с

T₅ = σ (t) / n = 1,24040,002с

T₆ = σ (t) / n = 1,34710,002с

T₇ = σ (t) / n = 1,67190,002с

I_{1 max} = 0,04315 кг*м 2 I_{1 min} = 0,04311кг*м 2

I_{2 max} = 0,03491 кг*м 2 I₂ _min = 0,03487кг*м 2

I_{3 max} = 0,02839 кг*м 2 I_{3 min} = 0,02835кг*м 2

I_{4 max} = 0,02261кг*м 2 I_{4 min} = 0,02257кг*м 2

I_{5 max} = 0,01816кг*м 2 I_{5 min} = 0,01812кг*м 2

I_{6 max} = 0,01491кг*м 2 I_{6 min} = 0,01487кг*м 2

I_{7 max} = 0,01267кг*м 2 I₇ _min = 0,01263кг*м 2

Теоретический расчет момента инерции прямого тонкого стержня длиной d и массой m относительно оси, перпендикулярной к стержню и проходящей через его середину находим по формуле (3.5).

s ( I ₀ )=(0.62 2 /12)*0.007= 0.0002 кг*м 2

Расчет погрешности косвенного измерения l 2 производим по формуле (3.5). Величину погрешности измерения l принимаем равной половине величины наименьшего деления шкалы расстояний или s ( l ) = 0,005.

Находим погрешности l 2 для каждого измерения:

1. s (l 2 )= 2*0,29*0,005=0,0029 м 2

2. s (l 2 )= 2*0,25*0,005=0,025 м 2

3. s (l 2 )= 2*0,21*0,005=0,0021 м 2

4. s (l 2 )= 2*0,17*0,005=0,0017 м 2

5. s (l 2 )= 2*0,13*0,005=0,0013 м 2

6. s (l 2 )= 2*0,09*0,005=0,0009 м 2

7. s (l 2 )= 2*0,05*0,005=0,0005 м 2

Экспериментальный расчет погрешностей косвенного измерения I произ-

водится по формуле (3.7), где s ( g )=0,01 и s (П)=0,01 (из справочников). s ( T )=1/10*0,002= 0,0002 (найдено по формуле (3.6). s ( l) = 0,005 половина деления прибора.

1. s ( I) = 0,0059≈0,006 кг*м 2

2. s ( I)= 0.0012≈0,001 кг*м 2

3. s (I)= 0.00082≈0,001 кг*м 2

4. s (I)= 0.00067≈0,001 кг*м 2

5. s (I)= 0.00064≈0,001 кг*м 2

6. s (I)= 0.00064≈0,001 кг*м 2

7. s (I)= 0.00067≈0,001 кг*м 2

I₀ =(0,358*0,62 2 )/12=0,0114 кг*м 2

Используя график на (рис.1) определим собственный момент инерции I₀ и массу стержня m:

b-это отрезок, который прямая линия графика отсекает от оси ординат (на вертикальной оси). Нужно определить ординату их точки пересечения. Но это правило справедливо в том случае, когда координатные оси пересекаются в начале координат, т.е. в точке с координатами (0;0). В нашем случае надо использовать другое правило: надо выбрать две точки на прямой, например точки с координатами и и записать уравнение прямой, проходящей через эти точки:

Приведение этого уравнения к виду y=ax+b дает следующие выражение для b:

Найденные из графика: собственный момент инерции I₀ и масса стержня m совпадают в пределах погрешности с теоретическими.

В результате проделанной работы мы убедились в справедливости теоремы Штейнера I = I₀ +ml 2 , так как смогли в пределах погрешностей измерений построить линеаризованный график зависимости I= f (l 2 ).

6.1. Как формируются понятия инерции материальной точки и твердого тела?

Моментом инерции материальной точки относительно неподвижной оси вращения называется физическая величина I, равная произведению массы m материальной точки на квадрат расстояния r ² до оси:

Момент инерции твёрдого тела относительно неподвижной оси вращения, складывается из моментов инерции отдельных его материальных точек:

6.2. В каких ситуациях применима теорема Штейнера?

Если известен момент инерции тела относительно любой оси проходящей через центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера.

6.3. Как формируется теорема Штейнера?

Момент инерции I относительно произвольной оси равен сумме момента инерции I 0 относительно оси, параллельной данной и проходящей через центр масс тела и произведения массы тела m на квадрат расстояния l между осями:

6.4. Под действием какой силы совершается колебательное движение маятника?

Под действием составляющей силы тяжести P1 = Psinφ .

6.5. Является ли момент инерции аддитивной величиной?

Является. Так как к аддитивным величинам относятся масса, энергия, импульс, момент импульса, объем, момент энергии.

6.6. Объяснить метод определения момента инерции с помощью физического маятника.

По основному закону динамики вращательного движения:

M = I∙β = — m∙g∙l∙φ (для малых углов отклонения); так как β = d 2 φ/dt 2 , то получаем дифференциальное уравнение гармонических колебаний:

, где ; период колебаний

; отсюда получаем выражение

Зная ускорение свободного падения g , массу m , экспериментально измерив l и определив Т , тогда можно вычислить момент инерции маятника .

6.7. Какой маятник называется физическим?

Физическим маятником называется любое твёрдое тело, которое под действием силы тяжести может свободно качаться вокруг неподвижной оси, не проходящей через центр масс.

6.8. При каких формальных допущениях справедлива формула (3,7)?

Период колебаний маятника равен:. Эта формула справедлива когда моментом силы трения можно пренебречь а также силой сопротивления воздуха, так маятник отклоняется на малые углы φ, то допускается sinφ ≈ φ.

6.9. Как записывается основной закон динамики вращательного движения?

Основной закон динамики вращательного движения записывается так: , что является аналитической формой основного уравнения (закона) динамики вращательного движения : при воздействии момента внешних сил твердое тело вращается вокруг неподвижной оси с угловым ускорением, прямо пропорционально моменту сил и обратно пропорционально моменту инерции тела относительно данной оси.