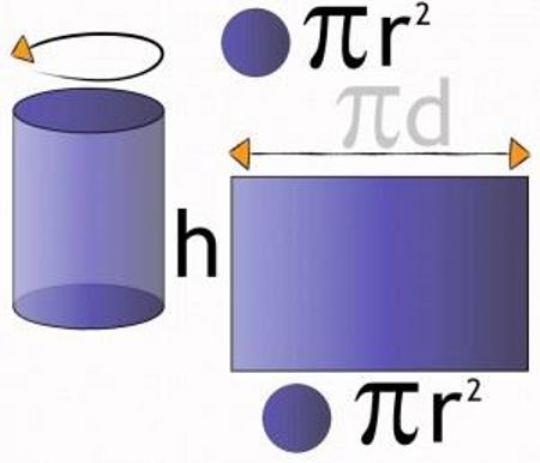
- Цилиндр: площадь боковой поверхности. Формула площади боковой поверхности цилиндра
- Понятие цилиндра
- Условные обозначения
- «Компоненты» стереометрической фигуры
- Основные формулы для работы с цилиндром
- Примеры с разобранным решением
- Задачи на закрепление материала
- Нахождение площади поверхности цилиндра: формула и задачи
- Формула вычисления площади цилиндра
- 1. Боковая поверхность
- 2. Основание
- 3. Полная площадь
- Примеры задач
- Площадь поверхности цилиндра
- Боковая поверхность цилиндра
- Площадь полной поверхности цилиндра
- Примеры расчета площади поверхности цилиндра
- Цилиндры
- Основные определения и свойства цилиндра
- Сечения цилиндра
- Объем цилиндра. Площадь боковой поверхности цилиндра. Площадь полной поверхности цилиндра
- 📽️ Видео
Видео:Цилиндр - расчёт площади, объёма.Скачать

Цилиндр: площадь боковой поверхности. Формула площади боковой поверхности цилиндра
При изучении стереометрии одной из главных тем становится «Цилиндр». Площадь боковой поверхности считается если не главной, то немаловажной формулой при решении геометрических задач. Однако важно помнить и определения, которые помогут сориентироваться в примерах и при доказательстве различных теорем.
Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Понятие цилиндра
Вначале нужно рассмотреть несколько определений. Только после их изучения можно приступать к рассмотрению вопроса о формуле площади боковой поверхности цилиндра. На основе этой записи можно вычислить и иные выражения.
- Под цилиндрической поверхностью понимают плоскость, описываемую образующей, движущейся и остающейся параллельной заданному направлению, скользящей по имеющейся кривой.
- Имеется и второе определение: цилиндрическую поверхность образуют множество параллельных прямых, пересекающих заданную кривую.
- Образующей называют условно высоту цилиндра. При ее перемещении вокруг оси, проходящей через центр основания, получается обозначенное геометрическое тело.
- Под осью подразумевают прямую, проходящую через оба основания фигуры.
- Цилиндром называется стереометрическое тело, ограниченное пересекающимися боковой поверхностью и 2 параллельными плоскостями.
Существуют разновидности данной объемной фигуры:
Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

Условные обозначения
- Радиус основания – R (он же заменяет аналогичную величину стереометрической фигуры).
- Образующая – L.
- Высота – H.
- Площадь основания – Sосн (иначе говоря, необходимо найти указанный параметр круга).
- Высоты скошенного цилиндра – h1,h2 (минимальная и максимальная).
- Площадь боковой поверхности – Sбок (если ее развернуть, то получится своего рода прямоугольник).
- Объем стереометрической фигуры – V.
- Площадь полной поверхности – S.
Видео:Видеоурок по математике "Цилиндр"Скачать

«Компоненты» стереометрической фигуры
Когда изучается цилиндр, площадь боковой поверхности играет немаловажную роль. Связано это с тем, что данная формула входит в несколько других, более сложных. Поэтому необходимо быть хорошо подкованным в теории.
Основными составляющими фигуры являются:
Читайте также: Порядок работы цилиндров двигателя рено 19
Видео:60. Площадь поверхности цилиндраСкачать

Основные формулы для работы с цилиндром
Для того чтобы ответить на вопрос, как найти площадь поверхности цилиндра, необходимо изучить основные «компоненты» стереометрической фигуры и формулы их нахождения. 
Видео:Нахождение площади боковой поверхности цилиндраСкачать

Примеры с разобранным решением
Необходимо узнать площадь боковой поверхности цилиндра. Дана диагональ сечения AC = 8 см (причем оно является осевым). При соприкосновении с образующей получается 








Видео:№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать

Задачи на закрепление материала
Дан цилиндр. Площадь боковой поверхности используется в дальнейшем решении. Известны другие параметры. Площадь основания – Q, площадь осевого сечения – М. Необходимо найти S. Иными словами, полную площадь цилиндра.
Читайте также: Индиан 4 цилиндра мотоцикл
Дан цилиндр. Площадь боковой поверхности необходимо найти в одном из шагов решения задачи. Известно, что высота = 4 см, радиус = 2 см. Необходимо найти полную площадь стереометрической фигуры. Источник
Видео:Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндраСкачать

Нахождение площади поверхности цилиндра: формула и задачи
В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.
Видео:Цилиндр, конус, шар, 6 классСкачать

Формула вычисления площади цилиндра
1. Боковая поверхность
Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту. Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом: Примечание: в вычислениях значение числа π округляется до 3,14.
2. Основание
В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна: Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:
3. Полная площадь
Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.: S = 2 π R h + 2 π R 2 или S = 2 π R (h + R)
Видео:ЗАДАНИЕ 8 из ЕГЭ_53Скачать

Примеры задач
Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см. Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см 2 . Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры. Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см 2 . Источник
Видео:Специфическая задача на площадь боковой поверхности цилиндраСкачать

Площадь поверхности цилиндра


Видео:ОТКУДА? Как найти площадь боковой поверхности конуса? Развёртка конуса | Математика с ДетекторомСкачать

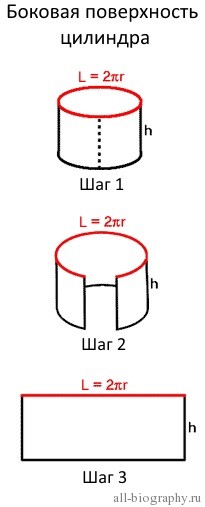
Боковая поверхность цилиндра
Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2). После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Верхнее основание исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr. На рисунке она отмечена красным цветом. Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника. Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.
Читайте также: Формула момент инерции цилиндра формула вывод
Видео:Почему площадь сферы в четыре раза больше её тени? [3Blue1Brown]Скачать
![Почему площадь сферы в четыре раза больше её тени? [3Blue1Brown]](https://i.ytimg.com/vi/JsrRqLK8zKg/0.jpg)
Площадь полной поверхности цилиндра
Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площадь полной поверхности цилиндра равна площадь верхнего основания цилиндра + площадь нижнего основания цилиндра + площадь боковой поверхности цилиндра или S = πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).
Видео:ЕГЭ СТЕРЕОМЕТРИЯ НАХОЖДЕНИЕ ПЛОЩАДИ БОКОВОЙ ПОВЕРХНОСТИ ЦИЛИНДРА ЧЕРЕЗ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ |Скачать

Примеры расчета площади поверхности цилиндра
Для понимания приведенных формул, попробуем посчитать площадь поверхности цилиндра на примерах. 1. Радиус основания цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра. Площадь боковой поверхности цилиндра равна 37,68. 2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6? S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4 S = 2 * 3,14 * 36 + 2 * 3,14 * 24 Площадь поверхности цилиндра равна 376,8. 3. Площадь боковой поверхности прямого кругового цилиндра равна 24π, а диаметр основания — 3. Найдите высоту цилиндра. Из формулы расчета площади боковой поверхности цилиндра Sбок. = 2πrh следует, что высота равна: Значение радиуса получаем из формулы: d = 2r Источник
Видео:11 класс, 17 урок, Площадь поверхности конусаСкачать

Цилиндры
Видео:Цилиндр и конус имеют общее основание и высоту. Высота цилиндра равна радиусу основания... (ЕГЭ)Скачать

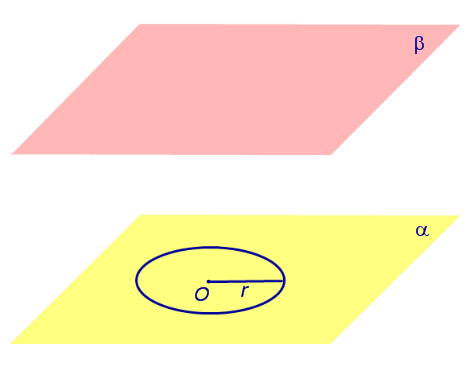
Основные определения и свойства цилиндра
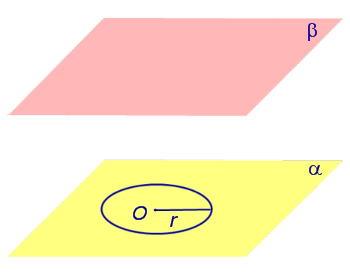
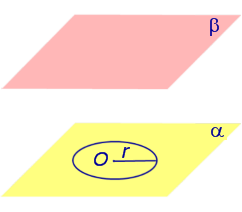
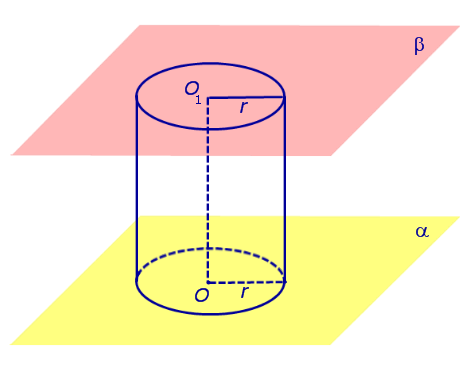
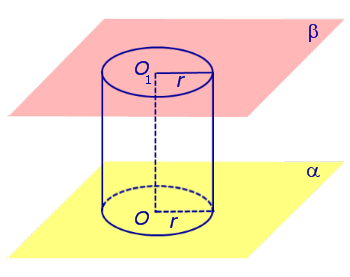
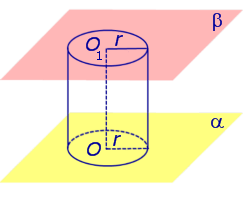
Видео:Площадь полной поверхности цилиндраСкачать

Сечения цилиндра
Определение 2. Сечением цилиндра называют пересечение цилиндра с плоскостью.
Если сечение проходит через ось цилиндра, то такое сечение называют осевым сечением цилиндра (рис. 3). 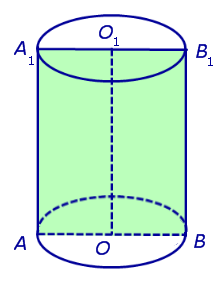
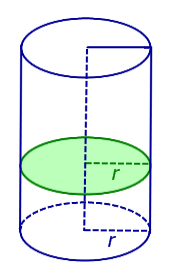
Видео:Урок 2. Площадь полной и боковой поверхности цилиндраСкачать

Объем цилиндра. Площадь боковой поверхности цилиндра.
Площадь полной поверхности цилиндра
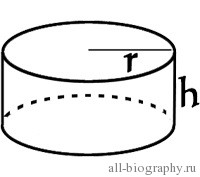
Для цилиндра с радиусом r и высотой h (рис. 5) 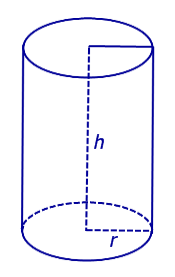
| V | объем цилиндра |
| Sбок | площадь боковой поверхности цилиндра |
| Sполн | площадь полной поверхности цилиндра |
| Sосн | площадь основания цилиндра |
Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности цилиндра: при помощи предельного перехода, когда число сторон правильной призмы n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы. Источник
📽️ Видео
РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать