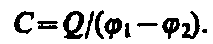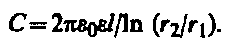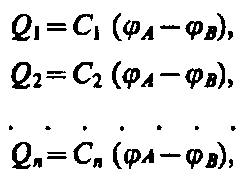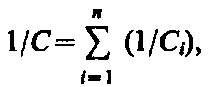Видео:Электрическая емкость. 10 класс.Скачать

Электроемкость уединенного проводника. Взаимная емкость двух проводников Конденсаторы.
Электрическая емкость уединенного проводника
Рассмотримуединенный проводник, т. е. проводник, который удален от других проводников, тел и зарядов. Его потенциал, согласн прямо пропорционален заряду проводника. Из опыта следует, что разные проводники, будучи одинаково заряженными, имеют различные потенциалы. Поэтому для уединенного проводника можно записать
(93.1)
называют электроемкостью (или просто емкостью) уединенного проводника. Емкость уединенного проводника определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу.
Емкость проводника зависит от его размеров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника. Это связано с тем, что избыточные заряды распределяются на внешней поверхности проводника. Емкость не зависит также ни от заряда проводника, ни от его потенциала.
Единица электроемкости — фарад (Ф): 1 Ф — емкость такого уединенного проводника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл.
Согласно (84.5), потенциал уединенного шара радиуса R, находящегося в однородной среде с диэлектрической проницаемостью e, равен
Используя формулу (93.1), получим, что емкость шара
(93.2)
Отсюда следует, что емкостью 1 Ф обладал бы уединенный шар, находящийся в вакууме и имеющий радиус R=C/(4pe0)»9×10 6 км, что примерно в 1400 раз больше радиуса Земли (электроемкость Земли С»0,7 мФ). Следовательно, фарад — очень большая величина, поэтому на практике используются дольные единицы — миллифарад (мФ), микрофарад (мкФ), нанофарад (нФ), пикофарад (пФ). Из формулы (93.2) вытекает также, что единица электрической постоянной e0 — фарад на метр (Ф/м) (см. (78.3)).
Для того чтобы проводник обладал большой емкостью, он должен иметь очень большие размеры. На практике, однако, необходимы устройства, обладающие способностью при малых размерах и небольших относительно окружающих тел потенциалах накапливать значительные по величине заряды, иными словами, обладать большой емкостью. Эти устройства получили названиеконденсаторов.
Если к заряженному проводнику приближать другие тела, то на них возникают индуцированные (на проводнике) или связанные (на диэлектрике) заряды, причем ближайшими к наводящему заряду Q будут заряды противоположного знака. Эти заряды, естественно, ослабляют поле, создаваемое зарядом Q, т. е. понижают потенциал проводника, что приводит (см. (93.1)) к повышению его электроемкости.
Конденсатор состоит из двух проводников (обкладок), разделенных диэлектриком. На емкость конденсатора не должны оказывать влияния окружающие тела, поэтому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют 1) две плоские пластины; 2) два коаксиальных цилиндра; 3) две концентрические сферы. Поэтому в зависимости от формы обкладок конденсаторы делятся наплоские, цилиндрические и сферические.
Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, возникающие на разных обкладках, являются равными по модулю разноименными зарядами. Подемкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (j1 —j2) между его обкладками:
(94.1)
Рассчитаем емкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга и имеющих заряды +Q и –Q. Если расстояние между пластинами мало по сравнению с их линейными размерами, то краевыми эффектами можно пренебречь и поле между обкладками считать однородным. Его можно рассчитать используя формулы (86.1) и (94.1). При наличии диэлектрика между обкладками разность потенциалов между ними, согласно (86.1),
(94.2)
где e — диэлектрическая проницаемость. Тогда из формулы (94.1), заменяя Q=sS, с учетом (94.2) получим выражение для емкости плоского конденсатора:
(94.3)
Для определения емкости цилиндрического конденсатора, состоящего из двух полых коаксиальных цилиндров с радиусами r1 и r2 (r2 > r1), вставленных один в другой, опять пренебрегая краевыми эффектами, считаем поле радиально-симметричным и сосредоточенным между цилиндрическими обкладками. Разность потенциалов между обкладками вычислим по формуле (86.3) для поля равномерно заряженного бесконечного цилиндра с линейной плотностью t =Q/l (l—длина обкладок). При наличии диэлектрика между обкладками разность потенциалов
Читайте также: Главный тормозной цилиндр ваз 213100
(94.4)
Подставив (94.4) в (94.1), получим выражение для емкости цилиндрического конденсатора:
(94.5)
Для определения емкости сферического конденсатора, состоящего из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу (86.2) для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов
(94.6)
Подставив (94.6) в (94.1), получим
Если d=r2—r1 2 /d. Так как 4pr 2 —площадь сферической обкладки, то получаем формулу (94.3). Таким образом, при малой величине зазора по сравнению с радиусом сферы выражения для емкости сферического а плоского конденсаторов совпадают. Этот вывод справедлив и для цилиндрического конденсатора: при малом зазоре между цилиндрами по сравнению с их радиусами в формуле (94.5) ln (r2/r1) можно разложить в ряд, ограничиваясь только членом первого порядка. В результате опять приходим к формуле (94.3).
Из формул (94.3), (94.5) и (94.7) вытекает, что емкость конденсаторов любой формы прямо пропорциональна диэлектрической проницаемости диэлектрика, заполняющего пространство между обкладками. Поэтому применение в качестве прослойки сегнетоэлектриков значительно увеличивает емкость конденсаторов.
Конденсаторы характеризуются пробивным напряжением — разностью потенциалов между обкладками конденсатора, при которой происходит пробой — электрический разряд через слой диэлектрика в конденсаторе. Пробивное напряжение зависит от формы обкладок, свойств диэлектрика и его толщины.
Для увеличения емкости и варьирования ее возможных значений конденсаторы соединяют в батареи, при этом используется их параллельное и последовательное соединения.
1. Параллельное соединение конденсаторов (рис. 144). У параллельно соединенных конденсаторов разность потенциалов на обкладках конденсаторов одинакова и равна jA – jB. Если емкости отдельных конденсаторов С1, С2, . Сn, то, согласно (94.1), их заряды равны
а заряд батареи конденсаторов
т. е. при параллельном соединении конденсаторов она равна сумме емкостей отдельных конденсаторов.
2. Последовательное соединение конденсаторов (рис. 145). У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи
где для любого из рассматриваемых конденсаторов Dji = Q/Сi. С другой стороны,
т. е. при последовательном соединении конденсаторов суммируются величины, обратные емкостям. Таким образом, при .последовательном соединении конденсаторов результирующая емкость С всегда меньше наименьшей емкости, используемой в батарее.
Видео:Лекция 131. Емкость цилиндрического конденсатораСкачать

Взаимная емкость двух цилиндров
Человеку (мне в частности), привыкшему к двухполюсникам, источникам эдс и замкнутым цепям трудно осознать понятие ‘емкости проводника’. Не взаимной емкости двух проводников, не конденсатора с двумя выводами, через который как бы течет ток, а просто висящей в воздухе емкости с одним контактом. Например, понятие ‘емкостной нагрузки антенны’ в виде каких-то замысловатых конструкций, никуда вторым концом не подключенных.
Для начала нужно отказаться от понятия емкости как хранилища энергии. Мол, чем больше емкость, тем больше в ней поместится энергии. Как хранилища заряда – да, но не энергии. Бесконечно малая точка содержащая заряд обладает нулевой емкостью, но бесконечной энергией. И наоборот проводник с бесконечной емкостью может принимать какой угодно заряд без затрат энергии, но и источником энергии после этого не станет. То есть емкость наоборот ‘размывает’, уменьшает энергию заряда. Выражается эта энергия через потенциал (тоже вечный вопрос, будоражащий умы, что есть потенциал, разность потенциалов, напряжение). Потенциал это та работа, которую нужно затратить, что перенести заряд из бесконечного далеко (то есть из точки без полей) в проводник c зарядом того же знака. Разные проводники с одинаковым зарядом обладают разным потенциалом. 1 кулон заряда загнанный в малый объем создает вокруг огромной величины поле, убывающее с расстоянием. Перенося другой 1 кулон издалека в тот же объем, мы сначала преодолеваем малое поле, потом больше, вблизи малого объема вообще огромное, прикладывая все большую силу, сумма произведений этой силы на расстояние на различных участках и есть работа, как мы знаем из механики. А в электростатике у нее есть синоним – потенциал. Если тот же 1 кулон был заперт не в малом объеме, а в приличных размеров шаре, то заряд распределится по большей поверхности, плотность его станет меньше и поле вблизи проводника меньше . Поэтому двигая другой заряд к этому проводнику из бесконечного далека мы сначала преодолеваем той же величины малое поле на таком же расстоянии как и раньше, но достигнем проводника раньше и не придется преодолевать гигантской величины поле на финальном этапе как в предыдущем случае. То есть совершим меньшую работу, затратим меньшую энергию и соответственно меньше энергии принесем в проводник. Заряд будет теперь тоже 2 кулона, как и при малом объеме, но будет обладать меньшей энергией, меньшим потенциалом. Величина характеризующая ‘размер шара’, его способность размывать энергию заряда, и есть емкость, величина обратная потенциалу. Это не то же самое, что ‘емкость конденсатора’, но родственные понятия.
Читайте также: Покраска алюминиевого блока цилиндров
Что будет, если мы приложим ‘батарейку’, источник эдс, одним концом к шару? Ничего не будет. Батарейка — это моторчик, способный передвинуть заряд из одного своего контакта на другой с заданной силой, добавить заряду потенциал, передвинуть его из точки с меньшим потенциалом в точку с большим. Но сама она источником зарядов не является, только может совершать работу по их перемещению. Вот чтобы в вышеописанном примере передвинуть заряд из бесконечного далека в шар батарейка бы сгодилась, если ее эдс выше потенциала шара и выше потенциала шара который получится после передвижения в него заряда. Так как же все-таки соединить вместе двухполюсный источник эдс и прочие привычные двухполюсные элементы с однополюсными емкостями? А возьмем второй шар и подключим второй контакт батарейки к нему. Незаряженный шар на самом деле содержит в себе носители заряда, и положительные и отрицательные, в огромном количестве, просто их количество одинаково, поэтому он и считается незаряженным. Теперь у источника эдс есть что двигать, он хватает один маленький заряд q и перемещает его из одного шара в другой, потенциал одного шара увеличивается от нейтрали в плюс на q/c1, другого в минус на -q/c2. Процесс повторяется. После переноса суммарного заряда Q разность потенциалов шаров становится u1-u2=Q/c1+Q/c2, сравнивается с эдс источника и он больше не в силах преодолеть разность потенциалов, поле между шарами. Заряд перестает перемещаться. В переложении на привычные для нас конденсаторы выглядит так, что мы подключили источник эдс к двум последовательным c1 и c2 и по ним протек какой-то ток I, передвинувший заряд Q=I*t и зарядил емкости до _разности_ потенциалов на каждой из них Q1/c1 и Q/c2. Хотя на самом деле никаких токов между шарами не было, мы даже не принимали в расчет их взаимовлияние друг на друга через поле, как будто они бесконечно удалены (поэтому было бы ошибкой проводить аналог шаров с обкладками конденсатора, это совершено другой эффект). Никакой _разницы_ потенциалов в пределах емкостей не было, были абсолютные потенциалы каждого шара относительно некоей абстрактной нейтрали. Но все равно результаты получили такие же, как с привычными для нас емкостями. Если считать ноль в розетке воткнутым в землю (большой шар), то можно фазу подключить к металлическому шарику диаметром 18 см (висящему где-нибудь далеко в космосе, чтобы игнорировать связь с землей через поле) и по этому одному проводу потечет ток, такой же как если бы мы воткнули в розетку обычный двухполюсный конденсатор 10пф. Пресловутая передача энергии по одному проводу
Что если рядом с шаром находится другой проводник? Нет, мы не переходим к конденсаторам, просто нейтральный проводник, мы не пытаемся перекачивать заряды с шара на него или обратно как в конденсаторе. Поле, создаваемое шаром, приводит к электростатической индукции в этом проводнике, в целом он остается нейтральным, но заряды в нем перераспределяются в пространстве таким образом, чтобы уменьшить поле, создаваемое шаром. Если рассматривать систему издалека, то в ней ничего не поменялось, суммарный заряд в системе из шара и другого проводника тот же, а пространственное перераспределение на таком расстоянии практически не сказывается и поле будет таким же. А вот вблизи системы все интереснее становится. Допустим шар заряжен отрицательно, тогда во втором проводнике у стороны ближней к шару скопятся положительные заряды, а у дальней отрицательные. Если рассматривать вклад каждого из этих перераспределившихся зарядов в поле около шара, получится что вклад положительных зарядов больше, поскольку они ближе, а значит, поле в сумме уменьшится, а значит, уменьшится энергия системы при том же суммарном заряде, а значит, увеличится емкость. Это мы пришли к понятию взаимной емкости, некоему подобию взаимной индуктивности в трансформаторе. Теперь у шара есть собственная емкость c1 и привнесенная c21 от соседствующего проводника. А у проводника, кстати, появляется собственный потенциал, несмотря на отсутствие собственного заряда, привнесенный через ту же ‘емкость связи’ c12=c21. Что любопытно, несмотря на перераспределение зарядов в проводнике и шаре, их поверхности остаются эквипотенциальными, то есть, несмотря на такое соседство и перекос поля, заряд по-прежнему донести хоть до передней хоть до задней точки шара стоит одинаковой энергии. Они именно так и перераспределяются, чтобы сохранить эквипотенциальность в исказившемся поле, исказить поле так, чтобы работа по преодолению поля до любой точки поверхности осталась той же. А вот что мне непонятно. Потенциал проводника высчитывают как собственный заряд поделить на собственную емкость плюс заряд соседнего проводника помноженный на емкость связи. Но! Мы же приблизили проводник с нулевым зарядом, а потенциал уменьшился. Нужно подумать. Подредактирую позже.
Вернемся к нашим двум шарам и источнику эдс. Вот теперь начнем учитывать емкость связи и тем самым перейдем к конденсатору. Емкость шара (в системе СГСЕ, чтобы всякие четыре-пи-эпсилон повсюду не пихать) равна просто его радиусу R (в системе СИ емкость шара радиуса 9мм примерно 1пф). Эффективная взаимная емкость системы двух шаров (без учета емкости связи), как было показано выше, эквивалентна их последовательному соединению, то есть R/2. Емкость связи двух шаров удаленных на расстояние N гораздо большее R равна R^2/2N (заметим, убывает линейно с расстоянием, а не квадратично как поле). Значит полная взаимная емкость R/2(1+R/N), то есть дает добавочку R/N*100 процентов к собственной емкости. Допустим пара шариков радиусом 1.6см на расстоянии 1.6м будут иметь взаимную емкость 1.01пф, из которых 0.01пф это емкость связи. Лишь на 0.01пф это ‘конденсатор’ а на 1пф все-таки собственная емкость шаров, абсолютная, не по отношению к чему-то. Точнее на 2пф емкость каждого, а на 1пф взаимная ‘последовательная’, но без учета поля друг друга.
Читайте также: Главный тормозной цилиндр тойота камри v30
В разных источниках по разному использую понятие ‘взаимная емкость’, в одних то что я обозначил как ‘емкость связи’, в других полную емкость, и собственную и связи. У меня ‘взаимная емкость’ — это именно полная.
В-общем устал я писать, возможно позже продолжу. Собственно писал я не для кого-то, а для себя. Привычка такая связно описать мысли в шпаргалках к экзаменам и не пользоваться ими потом, просто чтоб уложить все в мозгах получше. Дальше надо еще разобраться с взаимной емкостью частей одного проводника, которые я до того рассматривал лишь в статике, а в динамике то поле меняется не мгновенно а со скоростью света, потому емкость кусочков провода по отношению друг к другу приобретает серьезное значение, тем более что они то поближе друг к другу чем разнесенные на N>>R шары. В общем интересная тема. А ведь еще и диэлектрики есть кроме проводников.
Последний раз редактировалось rustot Вт дек 28, 2010 18:56:24, всего редактировалось 1 раз.
📸 Видео
Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Видеоурок по математике "Цилиндр"Скачать

Электроёмкость. Единицы электроёмкости. Конденсаторы | Физика 10 класс #52 | ИнфоурокСкачать

Объём цилиндраСкачать

Задание 51. Как начертить ЛИНИЮ ПЕРЕСЕЧЕНИЯ ПРИЗМ.Скачать

Урок 237. Электрическая емкость. КонденсаторыСкачать

Электроемкость. Конденсатор. 8 класс.Скачать

Электрический конденсатор и его ёмкость (видео 13) | Введение в электрические цепи | ЭлектротехникаСкачать
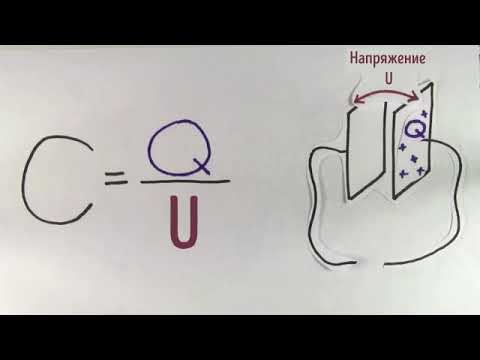
Геометрия конденсатора и его ёмкостьСкачать

Урок 238. Емкость плоского конденсатора. Классификация конденсаторовСкачать

Объем цилиндраСкачать

Полный обзор самого бюджетного измерителя ёмкости аккумулятора ZB2L3Скачать

Конденсаторы. Часть 2. ЕмкостьСкачать

Физика. Электроемкость уединенного проводникаСкачать

Конденсаторы пусковые МБГО 1 и МБГО 2Скачать