§ 25. Взаимное пересечение поверхностей геометрических тел
На чертежах деталей машин часто встречаются линии пересечения поверхностей, или, иначе, линии перехода. Поэтому необходимо изучить приемы построения этих линий.
Взаимное пересечение многогранников. На рис. 177, а приведены три изображения двух пересекающихся призм — четырехугольной и треугольной. Построение фронтальной проекции на рисунке не закончено; проекция линии пересечения на ней не показана. Требуется построить проекции линии пересечения на всех изображениях чертежа.
Рассматривая горизонтальную и профильную проекции, можно установить, что боковые грани вертикально расположенной призмы перпендикулярны горизонтальной плоскости проекций; проекция линии пересечения на эту плоскость совпадает с проекциями боковых граней, т. е. с отрезками прямых линий. Профильная проекция линии пересечения также совпадает с профильной проекцией треугольной призмы. Никаких дополнительных линий на этих проекциях не будет (рис. 177, б). Следовательно, решение задачи сводится к построению фронтальной проекции линии пересечения. Для этого нужно найти точку пересечения ребер одной призмы с гранями другой.
При решении задачи сначала определяют ребра каждой из призм, которые не пересекают грани другой (эти ребра на рис. 177, б не помечены цифрами). Затем, рассматривая профильную и горизонтальную проекции, видим, что ребра 1 — 2 и 3-4 пересекают наклонные грани треугольной призмы. Места пересечения-точки встречи ребер 1-2 и 3-4 с контуром профильной проекции треугольной призмы, т. е. а», b», с», d» видны на чертеже. Проекции невидимых точек заключены в скобки.
Горизонтальные проекции а, b, с, d точек A, В, С, D расположены на горизонтальных проекциях ребер 1-2 и 3-4. Проекции ребер изображаются в виде точек. Фронтальные проекции — точки а’ b’, с’, а’ определяют при помощи линий связи. Далее устанавливают, что ребра 5-6 и 7-8 треугольной призмы пересекают грани четырехугольной. Горизонтальные проекции точек пересечения е, f, g, h видны на чертеже. Фронтальные проекции точек Е, F, G, Н находят, проводя линии связи к проекциям соответствующих ребер. Чтобы получить линию пересечения, нужно соединить полученные точки прямыми линиями. Соединяют те точки, которые находятся на одних и тех же гранях каждой призмы. Затем нужно последовательно соединить точки а’, b’, g’, h’, d’, с’,f’, е’. Отрезки e’f’ и g’h’ — линии пересечения на фронтальной проекции — невидимы, так как закрыты наклонными гранями треугольной призмы, поэтому их обводят штриховой линией.
Наглядное изображение пересекающихся призм дано на рис. 177, в.
Рис. 177. Построение линии пересечения двух призм
На рис. 178 показано построение линии пересечения четырехугольной усеченной пирамиды и четырехугольной призмы. Построение выполнено аналогично приведенному на рис. 177. На фронтальной проекции линия пересечения совпадает с проекцией боковых граней призмы, так как они перпендикулярны фронтальной плоскости проекции (см. рис. 178). Верхнее и нижнее ребра призмы пересекаются с передним и задним ребрами пирамиды в точках 1, 2, 3, 4, проекции которых 1′, 2′, 3′, 4′ находятся в точках пересечения соответствующих ребер. Имея фронтальные и профильные проекции точек 1, 2, 3, 4, находят их горизонтальные проекции при помощи линий связи, как показано стрелками на чертеже.
Рис. 178. Построение линий пересечения четырехугольной призмы и усеченной пирамиды
Читайте также: Главный торм цилиндр 2110
Точки пересечения других двух ребер призмы с гранями пирамиды без дополнительного построения получить нельзя. Чтобы определить эти точки, призму и пирамиду пересекают горизонтальной секущей плоскостью Р. При пересечении плоскости Р с пирамидой образуется ромб, стороны которого будут параллельны сторонам оснований пирамиды. Ромб легко построить, спроецировав точку а’ на горизонтальную плоскость проекций и проведя прямые, параллельные сторонам основания. При пересечении плоскости Р с призмой образуется прямоугольник, равный горизонтальной проекции призмы. Точки 5, 6, 7, 8 пересечения контуров ромба и прямоугольника будут искомыми точками линий пересечения обоих тел.
Профильные проекции 5″, 6″‘, 7″, 8″ получены при помощи линий связи. В скобках проставлены проекции невидимых точек. Соединяя прямыми проекции точек, расположенных на одних и тех же гранях пирамиды и призмы, т. е. точки 1, 6, 2, 5, точки 3, 8, 4, 7, точки 1″, 5″, 2″ и точки 3″, 7″, 4″, получают недостающие проекции линии пересечения.
Взаимное пересечение тел вращения.
На рис. 179 показано построение линии пересечения двух цилиндров разных диаметров; оси цилиндров взаимно перпендикулярны и пересекаются.
На рис. 179, а изображены деталь, предназначенная для соединения труб,- тройник, и ее упрощенная модель — два пересекающихся цилиндра. Пересекаясь, цилиндрические поверхности образуют пространственную кривую линию. Горизонтальная проекция линии пересечения совпадает с горизонтальной проекцией вертикально расположенного цилиндра, т. е. с окружностью (рис. 179, б). Профильная проекция линии пересечения совпадает с окружностью, являющейся профильной проекцией горизонтально расположенного цилиндра. Отметив на горизонтальной проекции характерные точки 1, 2, 3, находят их профильные проекции 1″, 2″, 3″, которые расположены на дуге окружности. По горизонтальной и профильной проекциям точек 1, 2, 3 находят их фронтальные проекции 1′, 2′, 3′. Таким образом, находят проекции точек, определяющих линию перехода.
Видео:Как построить ЛИНИЮ ПЕРЕСЕЧЕНИЯ двух ЦИЛИНДРОВСкачать

В ряде случаев такого количества точек недостаточно, и чтобы получить дополнительные точки, применяют способ вспомогательных секущих плоскостей. Этот способ заключается в том, что поверхность каждого тела пересекают вспомогательной плоскостью, образующей фигуры сечений, контуры которых пересекаются. Точки, полученные при пересечении контуров сечений, являются точками линии пересечения. В данном случае оба цилиндра пересекают вспомогательной горизонтальной секущей плоскостью (рис. 179, в). При пересечении вертикально расположенного цилиндра образуется окружность, а горизонтально расположенного цилиндра — прямоугольник. Точки пересечения 4 и 5 окружности и прямоугольника принадлежат обоим цилиндрам и, следовательно, определяют линию пересечения обоих тел (см. рис. 179, а). Отметив профильные, а затем горизонтальные проекции точек 4 и 5, при помощи линий связи находят фронтальные проекции (см. рис. 179, в). Полученные точки соединяют плавной кривой.
При необходимости увеличить число точек, определяющих линию пересечения, проводят еще несколько параллельных вспомогательных секущих плоскостей.
Если оба цилиндра имеют одинаковые диаметры, то одна из проекций линий пересечения представляет собой пересекающиеся прямые (рис. 179, г и д), а линии пересечения — эллипсы.
Рис. 179. Построение линий пересечения цилиндров
Линия пересечения шара и прямого кругового цилиндра, ось которого проходит через центр шара, показана на рис. 180. Как видно из чертежа, на одной проекции линия пересечения изображается окружностью, а на другой проецируется в прямую линию.
Рис. 180, Линии пересечения шара и цилиндра
Проецирование тел с отверстиями. В технике встречаются детали с отверстиями цилиндрической, прямоугольной или какой-либо другой формы (рис. 181). При пересечении отверстий с поверхностями деталей образуются линии пересечения, форму которых в ряде случаев необходимо воспроизвести на чертеже. Задача эта решается в общем виде теми же способами, что и построение линий пересечения геометрических тел.
Читайте также: Схема устройства главного цилиндра сцепления урал 4320
Рис. 181. Детали с отверстиями
На рис. 182, а показан цилиндр с боковым отверстием цилиндрической формы. Оси цилиндра и отверстия пересекаются под прямым углом. Линия пересечения есть пространственная кривая. Построение линии пересечения было показано на рис. 179, а получение характерных точек данной кривой дано на рис. 182, а.
Линия пересечения цилиндра с отверстием прямоугольной формы при пересечении осей под прямым углом показана на рис. 182, б. Для построения линии пересечения на горизонтальной проекции выбраны характерные точки 1, 2, 3, 4, 5, 6. Профильные проекции 1″, 2″, 3″, 4″‘, 5″‘, 6″ расположены на окружности, являющейся проекцией цилиндра. Фронтальные проекции 1, 2′, 3′, 4′, 5′, 6′ находят по полученным горизонтальным и профильным проекциям. Соединив точки 1′, 2′, 3′, 4′, 5′, 6’ прямыми, получают ломаную линию пересечения в виде прямоугольной впадины.
На рис. 182, в показана линия пересечения цилиндра с отверстием, образованным четырехугольной призмой, и двумя полуцилиндрами. Такую форму имеет шпоночная канавка. Линия пересечения представляет собой прямолинейную впадину (см. рис. 182, б) с криволинейными краями (см. рис. 182, а).
Рис. 182. Чертежи цилиндров с боковыми отверстиями
Ответьте на вопросы
Видео:Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

1. В чем заключается способ вспомогательных секущих плоскостей? Для чего его применяют?
2. Какую форму имеет линия пересечения двух цилиндров разных диаметров и двух цилиндров одинаковых диаметров, если оси цилиндров пересекаются?
Задания к § 25 и главе IV
Упражнение 83
По двум данным проекциям детали начертите третью (рис. 183). Постройте недостающие проекции точек А и В, заданных проекциями а и b’ расположенных на видимых гранях. Выполните аксонометрическую проекцию, проставьте на ней размеры и нанесите точки А и Б.
Рис. 183. Задание для упражнений
Ответьте на вопросы
1. Какие проекции даны на чертеже?
2. Чему равны габаритные размеры детали?
3. Каковы размеры прямоугольного паза на детали?
4. Какова шероховатость поверхности, изображенной на главном виде штриховой линией?
5. Нужно ли обрабатывать основание детали и боковые стороны ?
6. Нужно ли обрабатывать верхнюю наклонную плоскость детали ?
Упражнение 84
По двум проекциям детали начертите третью (рис. 184). Постройте недостающие проекции точки, расположенной на видимой поверхности детали и заданной фронтальной проекцией d.
Видео:Задание 50. Построение ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ЦИЛИНДРОВСкачать

Рис. 184. Задание для упражнений
Ответьте на вопросы к рис. 184
1. Какова исходная форма детали?
2. Какие проекции даны на чертеже?
3. Что обозначают штриховые линии на фронтальной проекции ?
4. Что обозначают две горизонтальные штриховые линии на профильной проекции ?
5. Чем вызвано появление на фронтальной проекции двух вогнутых линий?
6. Можно ли без дополнительных построений обозначить на профильной проекции точку В, заданную фронтальной проекцией b’? Где находится эта точка на профильной проекции?
7. Каковы габаритные размеры детали?
8. Какие размеры определяет положение отверстия диаметром 40 мм?
9. Допустима ли обточка детали под размер 119,98 мм?
10. Допустима ли обточка детали под размер 119,8 мм? Если нет, то можно ли такой брак исправить?
11. Допустима ли обработка паза 60 мм под размер 60-0,1? Если нет, то можно ли такой брак исправить?
Читайте также: Главный цилиндр тормозной carib ae95
12. Нужно ли наносить размер между линиями, обозначенными цифрой 1 в зеленом четырехугольнике? В результате чего образовались эти линии?
13. Какова должна быть шероховатость большей части поверхности детали?
14. Какова шероховатость двух параллельных плоскостей в каждом из пазов?
Упражнение 85
Видео:Линия пересечения двух поверхностей вращения (Метод вспомогательных сфер)Скачать

По наглядным изображениям деталей (рис. 185, а-в) выполните чертежи в системе прямоугольных проекций. Масштаб чертежей возьмите 2 : 1. Размеры определите обмериванием наглядных изображений.
Ответы к упражнениям главы IV
| Обозначение | Наименование |
|---|---|
| 1 | Линия связи |
| 2 | Изображаемый предмет |
| 3 | Профильная проекция (вид слева) |
| 4 | Профильная плоскость проекций (W) |
| 5 | Фронтальная плоскость проекций (V) |
| 6 | Фронтальная проекция (вид спереди) |
| 7 | Горизонтальная плоскость проекций (Н) |
| 8 | Горизонтальная плоскость проекций (вид сверху) |
| 9 | Проектириующие лучи |
| А | Вид сперди (главный вид) |
| Б | Вид слева |
| В | Линия связи |
| Г | Вспомогательная прямая |
| Д | Вид сверху |
На примеры 1 и 2 ответы следующие (на примеры 3, 4, 5 ответы не приводятся):
В примерах 1 и 2 виды должны быть расположены так:
Пример решения задачи дан на рис. 277.
Рис. 277. Ответ к упражнению 57 (слева)
Пример решения задачи дан на рис. 278.
Рис. 278. Ответ к упражнению 58 (справа)
Чтобы выбрать правильное положение для главного вида, надо смотреть на детали по направлению, указанному стрелками со следующими буквами:
Пример выполнения задания дан на рис. 279.
Рис. 279. Ответ к упражнению 60
Технический рисунок детали показан на рис. 280.
Рис. 280. Ответ к упражнению 61
Видео:Проекции линии пересечения цилиндра с шаром Шар и цилиндр Взаимное пересечение шара с цилиндромСкачать

Пример решения на рис. 281.
Рис. 281. Пример ответа к упражнению 71
Пример решения на рис. 282.
Рис. 282. Пример ответа к упражнению 72
Пример решения на рис. 283.
Рис. 283. Пример ответа к упражнению 73
Детали, приведенные на рис. 159, целесообразно изобразить на главном виде в положениях, показанных на рис. 284, а и б
Рис. 284. Ответ на задания параграфа 22
Детали, представленные на рис. 163, рационально изобразить в положениях, показанных на рис. 285, а — в. Для втулки (рис. 163, а) достаточно одного вида, так как знак ∅ полностью выявляет ее форму. Для деталей, приведенных на рис. 163, б и в, необходимо по три вида. Чем это вызвано? Если дать для детали, изображенной на рис. 163, в, главный вид и вид слева, то останутся неясными форма четырех срезов по углам и вертикальных пазов спереди и сзади детали. Без вида сверху срезы можно представить себе не как фаски, а как прямоугольные вырезы и т. п.
Форма пазов без вида сверху также не выявляется. Можно предположить, что они полукруглые, овальные, треугольные и т. д. Если же дать главный вид и вид сверху, то форма этих элементов будет точно определена. Но тогда не будет ясна форма горизонтального паза. Без вида слева можно сделать различные предположения о его форме. Поэтому, в данном случае, необходимы три вида. Примерно то же относится и к детали, изображенной на рис. 163, б.
Разъяснения к вопросу о рациональной планировке поля чертежа даны на рис. 286.
Рис. 286. Ответ на задание к § 22
Правильно выполненные эскизы приведены на рис. 287.
Видео:Задание 54. Чертеж ЛИНИИ ПЕРЕСЕЧЕНИЯ цилиндра и призмы трехгранной Часть 1Скачать
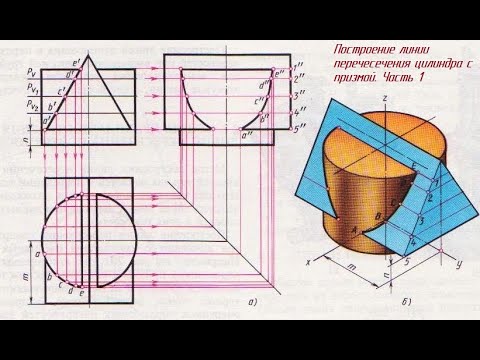
Рис. 287. Ответ на упражнения 80
Правильно выполненные эскизы приведены на рис. 288.
Рис. 288. Ответ к упражнению 82
📽️ Видео
Задание 54. Аксонометрия ЛИНИИ ПЕРЕСЕЧЕНИЯ цилиндра и призмы трехгранной Часть 2Скачать
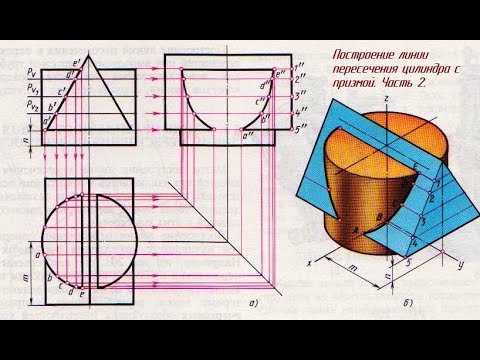
Пересечение поверхностей полусферы и цилиндра. Пошаговое видео. Инженерная графикаСкачать

Пересечение конуса и цилиндраСкачать

Линии пересечения цилиндра с шаром. Проекции взаимного пересечения шара с цилиндром.Скачать

Как построить ЛИНИИ ПЕРЕСЕЧЕНИЯ трехгранной ПРИЗМЫ С ЦИЛИНДРОМСкачать

Взаимное пересечение поверхностей/ (способ секущих плоскостей)/ Задача 49./ Рабочая тетрадь.Скачать

Построение линии пересечения конуса вращения с цилиндром вращения. Анимация.Скачать

Линия пересечения конуса и цилиндра (метод концентричных секущих сфер)Скачать

Задачи 4.3.10 и 4.3.11.Скачать

РТ_ПБ_61.1) Построить проекции линии пересечения цилиндра плоскостью частного положения.Скачать

Лекция 12. Пересечение поверхностей метод плоскостейСкачать

Задание 51. Как начертить ЛИНИЮ ПЕРЕСЕЧЕНИЯ ПРИЗМ.Скачать

Пересечение двух цилиндров. Инженерная графикаСкачать





























