За площадь боковой поверхности цилиндра принимается площадь ее развертки

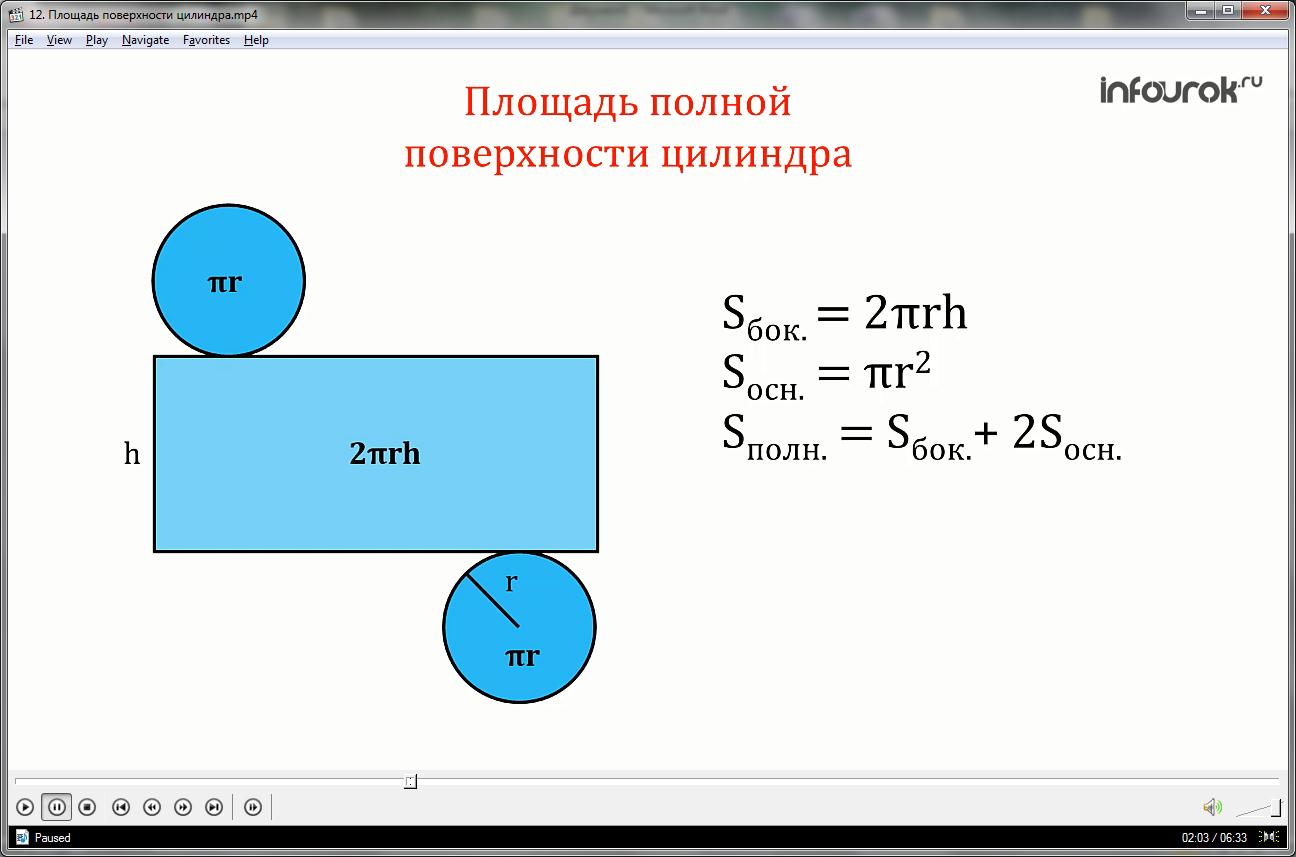
За площадь боковой поверхности цилиндра принимается площадь ее развертки.

Так как площадь прямоугольника АВВ₁А₁ равна , то для вычисления площади S_бок боковой поверхности цилиндра радиуса г и высоты h получается формула: .

Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. Так как площадь каждого основания равна πr 2 , то для вычисления площади полной поверхности цилиндра получаем формулу:

Задача 1. Площадь боковой поверхности цилиндра равна S. Найти: площадь осевого сечения цилиндра (рис.57)

Решение: . По рисунку (рис. 57) площадь осевого сечения – это площадь прямоугольника ABCD. .

Из формулы нахождения площади боковой поверхности: . Подставим это выражение в формулу осевого сечения: .

Задача 2.Сколько квадратных метров листовой жести пойдет на изготовление трубы длиной 4 м и диаметром 20 см, если на швы необходимо добавить 2,5% площади ее боковой поверхности?.

Решение. Воспользуемся формулой площади полной поверхности цилиндра: .

Радиус равен половине диаметра – 0,1м, а высота цилиндра равна длине нужной трубы – 4м.

Так на швы нужно добавить 2,5% площади ее боковой поверхности, нужно найти: (S+2,5%S). Подставим вместо S формулу площади боковой поверхности, и вычислим:

Конспект урока «Площадь поверхности цилиндра»

Ищем педагогов в команду «Инфоурок»

Тема урока: Площадь поверхности цилиндра.

Цель урока: познакомить с формулами нахождения площади боковой и полной поверхности ци­линдра, вырабатывать навыки применения теоретических знаний к решению типовых задач по данной теме ; развивать пространственное представления, логическое мышление, умения анализировать, делать выводы, культуру математической речи; развитие коммуникативных умений: умение слушать и слышать, правильно задавать вопросы; воспитание ответственного отношения к учебному труду, умения высказывать свое мнение, воспитание умения участвовать в диалоге, самостоятельности.

Тип урока: усвоение новых знаний.

Оборудование: мультимедийный комплекс, презентация, модели цилиндра, раздаточный материал.

Организуется начало урока. Активизируется внимание учащихся на начало учебного процесса. Демонстрируется готовность к началу урока.

2. Формулирование темы, цели и задач урока. Мотивация учебной деятельности.

Мы продолжаем изучение цилиндра. Цилиндр – первая фигура вращения, которую мы изучили. В дальнейшем мы изучим еще две фигуры, полученные аналогичным путем. Многие предметы в окружающем мире представляют собой цилиндр. Его изучение поможет решать практические задачи, возникающие в нашей жизни. Данная тема также включена в задания ЕГЭ.

Сегодня мы познакомимся с новыми фактами, относящимися к цилиндру и новые знания вы будете добывать сами. А работать мы будем под девизом: «Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не памятью».

3.Актуализация опорных знаний.

1)Какая фигура называется цилиндром?

2) Почему цилиндр называют телом вращения?

Читайте также: Главный тормозной цилиндр газ 53 в украине

3) Назовите виды цилиндров?

4) Назовите элементы цилиндра.

5) Что представляет собой развертка цилиндра?

6) Назовите основные виды сечений цилиндра. Какая фигура получается в каждом случае?

7) Приведите примеры использования цилиндров.

Учащиеся сверяют ответы и оценивают свою работу.

Сколько потребуется краски, чтобы покрасить бак цилиндрической формы с диаметром основания 1,5 м и высотой 3 м, если на один квадратный метр расходуется 200 г краски?

-В задаче мы имеем дело с цилиндром.

-Что необходимо знать, чтобы найти количество краски? ( Необходимо знать площадь полной поверхности цилиндра?)

-Из чего будет складываться площадь полной поверхности цилиндра? ( Площадь боковой поверхности и двух оснований)

-Мы попробуем сейчас это сделать.

— Как вы думаете, что принимается за площадь боковой поверхности цилиндра? ( За площадь боковой поверхности цилиндра принимается площадь её боковой развертки)

— Что является разверткой боковой поверхности цилиндра?

-Отдельно в цилиндре выделяют боковую поверхность и основания. Чтобы более наглядно представить боковую поверхность, возьмём лежащий на столе лист бумаги и свернём в виде свитка. Теперь вернём лист в первоначальное положение. Какую геометрическую фигуру вы получили? Этот прямоугольник называют развёрткой боковой поверхности цилиндра.

б)Как вы думаете, чему равна площадь боковой поверхности?

Предложить учащимся доказать теорему о площади боковой поверхности цилиндра.

(Учащиеся приводят доказательство, основываясь на том, что за площадь боковой поверхности цилиндра принимают площадь его развёртки, т.е. прямоугольника, и приходят к формуле: S= 2пrh). Вывод и доказательство учащиеся записывают в тетрадь.

в) Чем образована полная поверхность цилиндра? По какой формуле можно вычислить её площадь? (S= 2пrh +2пr 2 ).

5. Первичное закрепление нового материала.

1)Решение задач по готовым чертежам.

2) Вернемся к задаче о которой говорили в начале урока.

Сколько потребуется краски, чтобы покрасить бак цилиндрической формы с диаметром основания 1,5 м и высотой 3 м, если на один квадратный метр расходуется 200 г краски?

Учащиеся записывают решение в тетрадь:

S полн . =2 π r( r + h ) = 2 . 3,14 . 0,75 . (0,75 + 3) = 17,6625 (м 2 ),

-Как вычислить количество краски?

Надо площадь полной поверхности цилиндра умножить на количество краски на один квадратный метр .

3)Решение задачи исследовательского характера

Две цилиндрические детали покрывают слоем никеля одинаковой толщины. Высота первой детали в 2 раза больше высоты второй, но радиус её основания в 2 раза меньше радиуса основания второй детали. На какую из деталей расходуется больше никеля?

ü Введем обозначения : h₁ ,h_{2 –}высоты деталей;

ü Запишите соответствие высот и радиусов данных деталей;

ü Запишите формулы полной поверхности цилиндров;

ü Сравните полученные площади

Ответ: на вторую деталь никеля потребуется больше

Самостоятельная работа проводится по вариантам, дифференцированно, с выбором ответа.

Фамилия, имя ученика_____________________________

Реши задачи и выбери правильный ответ, заполни таблицу.

Читайте также: Задний тормозной цилиндр менять парой

№1. Радиус основания цилиндра равен 2 см, высота – 5 см, тогда площадь боковой поверхности равна:

№2. Радиус основания цилиндра равен 3 см, высота – 6 см. Найти площадь полной поверхности цилиндра.

№3. Если площадь боковой поверхности цилиндра равна 64π кв.м, а высота – 4 м, тогда радиус равен:

№4. Во сколько раз увеличится площадь боковой поверхности цилиндра, если его высоту и радиус увеличить в три раза?

Фамилия, имя ученика_____________________________

Реши задачи и выбери правильный ответ, заполни таблицу.

№1. Осевым сечением цилиндра является прямоугольник со сторонами 12 и 8 см, то площадь боковой поверхности цилиндра может быть равна:

№2. Во сколько раз уменьшится площадь боковой поверхности цилиндра, если его высоту уменьшить в 4 раза, а радиус увеличить в 2 раза?

1) не изменится; 2) 8; 3) 4; 4) 2

№3. Длина окружности основания цилиндра равна 3.Площадь боковой поверхности равна 6.Найдите высоту цилиндра.

№4. Площадь полной поверхности цилиндра, полученного вращением прямоугольника со сторонами 4 см и 7 см вокруг его большей стороны, равна:

Проверка самостоятельной работы ( взаимопроверка)

7. Подведение итогов урока.

Подведем итог работы на уроке.

Ø С какими новыми понятиями вы сегодня познакомились?

Ø Значима ли для нас данная тема?

Ø Где мы можем ее применить?

Ø Как мы можем оценить полученные нами знания? Усвоили ли мы их?

Ø Как вы думаете, люди каких профессий могут использовать знания, полученные при изучении цилиндра?кий

Ø 8. Домашнее задание. Выучить теоретический материал п. 60, решить задачи № 537,№540.

Найти площадь боковой поверхности цилиндра, если его радиус равен R , a образующую видно из центра основания под углом α.( Ответ: 2π R 2 tg α)

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Урок «Площадь поверхности цилиндра»

Краткое описание документа:

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

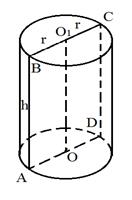
Поверхность цилиндра состоит из боковой поверхности, и оснований цилиндра, которые представляют собой два круга.

Длина образующей боковой поверхности называется высотой цилиндра (АВ), а радиус основания — радиусом цилиндра.

Попробуем разрезать боковую поверхность нашего цилиндра по образующей АВ так, чтобы все образующие оказались в плоскости α.

В результате в плоскости α получился прямоугольник ABCD. Этот прямоугольник представляет собой развертку боковой поверхности цилиндра.

Сторона AD – развертка окружности основания цилиндра, а высота АВ — образующей цилиндра.

AD= (формула длины окружности)

где r — радиус окружности, h — высота цилиндра.

За площадь боковой поверхности цилиндра принимается площадь ее развертки, т.е. площадь прямоугольника АВСD.

Площадь прямоугольника находится по формуле:

площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра.

Читайте также: Кубик кирпичик призма пластина цилиндр

Найдем площадь полной поверхности цилиндра.

Цилиндр состоит из боковой поверхности и двух оснований.

Площадь полной поверхности цилиндра равна сумме площади двух оснований и боковой поверхности.

Так как основания в цилиндре равны, то полная его площадь будет рассчитываться по формуле:

Полученные знания применим при решении задач.

Трубка цилиндрической формы получается из прямоугольника. Вычислите радиус основания, если длина прямоугольника равна 16 см, ширина – 12см.

Так как трубка получается из прямоугольника, то его длинна – это есть длина окружности.

Найдем радиус окружности: (отношение длины окружности к двум пи)

Дано: цилиндр, ABCD-осевое сечение, АС=48 см, ACD= 60º.

Найти: а) СD — высота, б) АО — радиус, в) Sосн.

а)1.Рассмотрим осевое сечение АВСD.

ABCD — прямоугольник (по условию), значит

АС — гипотенуза, СD — катет, лежащий против угла в 30⁰.

Он равен половине гипотенузы

АО – радиус основания цилиндра.

АD – диаметр основания цилиндра. Поэтому, найдем диаметр по формуле

У отдельных изваяний, оставленных нам древнеегипетской культурой, можно видеть зажатые в руках объекты цилиндрической формы, предназначение которых историкам непонятно.

В 1976 году в Закавказье обнаружена старинная рукопись «Тайны Жизни и Смерти», в которой содержалась информация о Лунном и Солнечном цилиндрах, изготовленных из цинка и меди с определенным внутренним наполнением.

Было установлено, что цилиндры Фараона, так они называются, обладают широчайшим спектром благотворного воздействия на организм человека.

В него входят: помощь при сердечно-сосудистых заболеваниях, нейротрофических, гипертонии, болезнях выводящих путей, астме, бессоннице, головных болях, а также в качестве средства для снятия стрессов и профилактики атеросклероза.

Согласно мнению ряда врачей, Цилиндры Фараона представляют собой уникальный, самонастраивающийся на каждого человека, физиотерапевтический прибор, созданный гением древнеегипетских ученых.

Исследования показали, что воздействие Цилиндров Фараона переводит организм в иное, более «высокое» энергетическое состояние, при котором активнее протекают восстановительные процессы, способствующие гармонизации всего организма.

АвторДата добавленияРазделПодразделПросмотровНомер материала

Инфоурок

07.11.2014

Геометрия

Видеоурок

11843

998

© 2021 Проект «Уроки математики»

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.

🌟 Видео