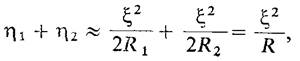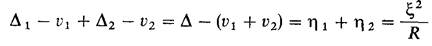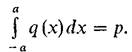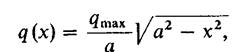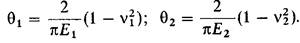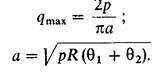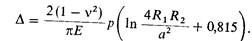Задача герца для двух цилиндров (7 видео)

Содержание

Контакт цилиндров из однородных материалов. Схема контакта двух цилиндров
контактные напряжения
2.2.2.1 Постановка задачи Герца
📸 Видео

Видео:Механическое Напряжение. Расчеты на прочность и жесткость. Формула герцаСкачать

Контакт цилиндров из однородных материалов. Схема контакта двух цилиндров

Схема контакта двух цилиндров

Контактные напряжения

Контактными называют напряжения в зоне контакта деталей машин. На практике часто появляется необходимость определения напряжений и деформаций в этих зонах как при расчете на контактную прочность (зубчатые и фрикционные передачи), так и для оценки предела выносливости (резьбовые и прессовые соединения и др.).

Конструкционные контактные задачи решают методами теории упругости, как правило, приближенно. Достаточно точные решения получены лишь для задач об упругом контакте деталей простой формы (цилиндры, шары и т. п.).

Для понимания принципиального подхода при решении контактных задач рассмотрим взаимодействие цилиндров (задача Герца).

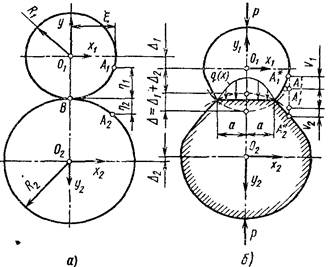
Рассмотрим напряженное состояние двух длинных цилиндров с параллельными осями (а), сжатых распределенными по длине радиальными нагрузками р (б). На расстоянии x от плоскости, проходящей через оси цилиндров, возьмем две точки A1 и А2,. Если контакт цилиндров без нагрузки происходил по линии, параллельной их осям через точку В, то расстояние между этими точками вдоль оси у равно (см. рис.а)

Условие совместности перемещений*

R1 и R2. — радиусы первого и второго цилиндров; R — «средним» радиус кривизны 1/R = 0,5(1/R+ 1/R) ;

Под действием распределенной нагрузки р произойдет деформация цилиндров в зоне контакта, а их оси переместятся к этой зоне на величины D1, и D2. Общее сближение осей (см. рис. б) D = D1 + D2. Точки займут новое поверхности цилиндров, получив перемещения положение А¢1 и А¢2. , а точки, равные v1 и v2, займут положения A*1 и А*2. В зоне контакта точки А*1 и А*2 совместятся и потому

Это равенство выражает условие совместности перемещений контактирующих точек цилиндров и показывает, что перемещения осей цилиндров под нагрузкой вызывают смещения точек в результате деформации.

Распределение давлений по площадке*

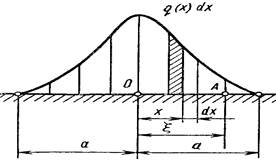
Если трение отсутствует, то в точках контакта будут действовать лишь нормальные давления q (x), и условие равновесия примет вид

Выражая смещения v через контактные давления q, используя модуль упругости Е и коэффициент Пуассона n по теории упругости (задача Фламана), имеем закон распределения давлений по ширине

где а –половина ширины контакта

Если цилиндры изготовлены из материалов, у которых Е1 = E2 и n1 = n2 = 0,3, то

Читайте также: Антифриз в цилиндрах рено логан

Так как полуширина контактной площадки а зависит от р, то смещение D является нелинейной функцией от р, хотя материал цилиндров предполагается упругим. Это объясняется изменением а в процессе нагружения: значение а возрастает по мере увеличения р, и относительная податливость контактной зоны уменьшается.

Эта задача, впервые решенная Г. Герцем, широко применяется в расчетах на контактную прочность деталей ‘машин конечной длины(фрикционных и зубчатых передач и др.)..

Видео:10 Задача Герца. Контакт цилиндра и плоскостиСкачать

контактные напряжения

КОНТАКТНЫЕ НАПРЯЖЕНИЯ механические — напряжения, к-рые возникают при механич. взаимодействии твёрдых деформируемых тел на площадках их соприкасания и вблизи площадок (напр., при сжатии соприкасающихся тел). Знание К. н. важно для расчёта на прочность подшипников, зубчатых и червячных передач, шариковых и цилиндрич. катков, кулачковых механизмов и т. п. Определение К. н. составляет задачу, наз. контактной.

Решение нек-рых контактных задач для упругих тел впервые дано Г. Герцем (G. Hertz). В основу его теории К. н. положены след, предположения: материал соприкасающихся тел в зоне контакта однороден и следует закону Гука; линейные размеры площадки контакта малы по сравнению с радиусом кривизны и линейными размерами соприкасающихся поверхностей в окрестности точек контакта; силы трения между соприкасающимися телами пренебрежимо малы. При этом найдено, что при сжатии двух тел, ограниченных плавными поверхностями, площадка контакта имеет форму эллипса (в частности, круга или полоски), а интенсивность распределения К. н. по этой площадке следует эллипсоидальному закону.

К. н. имеют местный характер, т. е. быстро убывают при достаточном удалении от места контакта (соприкасания тел). Распределение К. н. по площадке контакта и в её окрестности неравномерно и характеризуется большими градиентами. Важной особенностью распределения К. н. (напр., при сжатии шаров или пересекающихся цилиндров) является то, что макс, касательные напряжения к-рые в значит. мере предопределяют прочность сжимаемых тел, имеют место на нек-рой глубине под площадкой контакта. Вблизи самой этой площадки напряжённое состояние близко к гидростатич. сжатию, при к-ром, как известно, касательные напряжения отсутствуют.

Рис. 1. Возникновение контактных напряжений при соприкосновении шаров.

Рис. 2. Возникновение контактных напряжений при соприкосновении цилиндров.

Характерными случаями соприкасания упругих тел являются следующие.

1) Соприкасание шаров (рис. 1); площадка контакта имеет форму круга радиуса а, на к-ром действует давление с интенсивностью

(i = l, 2) — модуль Юнга материала рассматриваемых тел, — коэф. Пуассона, Р — равнодействующая сил, приложенных к каждому из соприкасающихся шаров, R 1 и R 2 — радиусы кривизн соприкасающихся поверхностей. Наибольшие сжимающие К. н. (рис. 1, б) действуют в центре площадки и равны а между напряжениями в центре площадки контакта существует зависимость Макс. касательные напряжения в этом случае равны и имеют место в точке А, отстоящей от центра площадки контакта по оси на расстоянии 0,786 а.

2) Соприкасание двух цилиндров (рис. 2), оси к-рых образуют угол площадка контакта — эллипс; интенсивность распределения давления по этой площадке определяется ф-лой

Читайте также: Давление цилиндров рено логан

Эксцентриситет эллипса е определяется из соотношения

К(е), Е(е) — полные эллиптич. интегралы 1-го и 2-го рода.

Если угол а R 1 =R 2 (рис. 2, б), то площадка контакта будет кругом и закон распределения давления по ней будет таким же, как и в случае сжатия шаров. Характерно, что макс. К. н. при сжатии двух шаров радиуса R примерно в 1,6 раза больше макс. К. н. при сжатии двух накрест лежащих цилиндров радиусы к-рых равны R, а материал и равнодействующая Р такие же, как и у шаров.

Если то большая ось площадки контакта между соприкасающимися цилиндрами увеличивается и при (или при становится сравнимой с радиусом цилиндра. В этом случае ф-лы для определения деформаций, полученные в теории Герца, не применимы. Однако ф-лы, полученные на основании этой теории (когда область контакта мала), имеют смысл и в этом случае, т. е. при В случае (рис. 2, в)площадка контакта имеет вид полоски шириной 2l. Распределение давления по этой полоске определяется ф-лой

где Q — нагрузка на единицу длины цилиндра.

Теория Герца и проблема К. н. в целом получили значительное матем. развитие в течение последних двух-трёх десятилетий, что позволило изучить влияние сил трения между соприкасающимися телами на величину К. н.; исследовать случаи соприкасания тел, когда одно из них является гибким, напр. плиты и балки на упругом основании, подкрепляющие кольца и стержни; рассмотреть случаи, когда линейные размеры области контакта сравнимы с радиусом кривизны соприкасающихся тел, напр. давление цилиндра на край цилиндрич. отверстия в упругом теле, радиусы к-рых почти равны; решена задача в общем случае о давлении абсолютно жёсткого тела (штампа), круглого в плане, на упругое полупространство; решены нек-рые конкретные задачи для анизотропных тел и ряд др. задач.

Читайте также: Нумерация цилиндров двигателя v6 ягуар

Лит.: Рвачев В. Л., Проценко B. C., Контактные задачи теории упругости для неклассических областей, К., 1977; Моссаковский В. И., Гудрамович В. С., Макеев Е. М., Контактные задачи по теории оболочек и стержней, М., 1978; Галин Л. А., Контактные задачи теории упругости и вязкоупругости, М., 1980; Попов Г. Я., Концентрация упругих напряжений возле штампов, разрезов, тонких включений и подкреплений, М., 1982; Александров В. М., Мхитарян С. М., Контактные задачи для тел с тонкими покрытиями и прослойками, М., 1983; Теплый М. И., Контактные задачи для областей с круговыми границами, Львов, 1983. В. В. Панасюк.

Видео:Скатывание цилиндров с наклонной плоскостиСкачать

2.2.2.1 Постановка задачи Герца

При контакте кантилевера и образца вступают в действие упругие силы. Возникают деформации как образца, так и зонда, которые могут влиять на получаемую при сканировании картину. Для правильной интерпретации результатов и выбора режима исследования необходимо иметь представление об упругих взаимодействиях в контактном и «полуконтактном» режимах.

Такое рассмотрение необходимо для того, чтобы:

избежать разрушения зонда или образца при сканировании. Ведь даже при слабой прижимающей силе давление в области контакта может превысить предел прочности, т.к. контактная площадка очень мала;
на основе полученного профиля правильно восстановить форму поверхности образца в случае, когда детали на ней по размеру сравнимы с радиусом закругления острия зонда;
в «полуконтактном» режиме анализировать силы в момент касания зондом поверхности, которые непосредственно влияют на колебания кантилевера и являются одной из причин затухания.

Упругие деформации в контакте (задача Герца).

Для начала рассмотрим только силу упругости. Нахождение деформаций при локальном соприкосновении тел при воздействии нагрузки составляет задачу Герца.

Сделаем несколько упрощающих предположений [1].

Допустим, что материалы, как образца, так и кантилевера, изотропны, а значит, все их упругие свойства описываются всего двумя парами параметров – модулями Юнга , и коэффициентами Пуассона , . (В анизотропном случае число таких независимых упругих характеристик может достигать 21).
Считаем, что вблизи точки соприкосновения недеформированному участку поверхности каждого из тел можно приписать два радиуса кривизны , (для зонда) и , (для исследуемого участка образца) во взаимно перпендикулярных плоскостях, ортогональных самой поверхности в данной точке (рис. 1).
Деформации малы по сравнению с радиусами кривизны поверхностей.