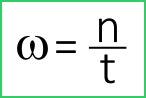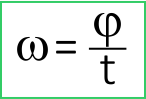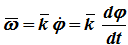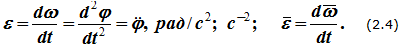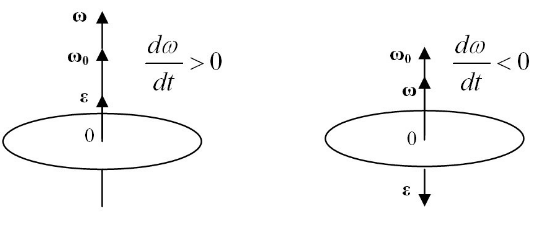Задачи на вращательное движение тела

Цилиндр 1, масса которого m_ц=78 кг и диаметр d=24 см, может свободно вращаться около горизонтальной оси. На цилиндр намотана гибкая нить, имеющая на конце груз 2 массой m_гр=10 кг. Падая, груз разматывает нить и вращает цилиндр (рис. 269, а).

Определить угловое ускорение цилиндра, натяжение нити, кинетическую энергию груза A и цилиндра через t=4 сек после начала движения.

Массой нити и трением в оси цилиндра пренебречь.

Видео:Урок 100. Задачи на вращение твердого тела (ч.1)Скачать

Решение (при помощи метода кинетостатики и уравнения основного закона динамики для вращающегося тела)

1. В задаче рассматриваются два связанных между собой тела: вращающийся цилиндр и поступательно двигающийся груз. Мысленно разрежем нить и изобразим оба тела с действующими на них силами отдельно друг от друга.

2. На рис. 269, б показан цилиндр, на который действует вращающий момент пары сил (T, T₁), созданной натяжением нити (сила T₂ приложена к подшипнику цилиндра, см. § 45):

Видео:Вращательное движение твёрдого тела. Задачи 1, 2, 3Скачать

Решение 2 (при помощи закона кинетической энергии)

1. Второе решение начинается с того, чем заканчивается первое.

Через t=4 сек оба тела приобретают кинетическую энергию благодаря работе, произведенной грузом 2 при падении с высоты h (рис. 270).

6. Так как значение углового ускорения ε известно, легко найти величины кинетических энергий E_ц и E_гр (см. п. 2 решения).

Видео:Вращательное движение. 10 класс.Скачать

iSopromat.ru

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела:

Видео:Кинематика вращательного движения. ТермехСкачать

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющаяся приращением угла поворота тела за промежуток времени.

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

• если известно количество оборотов n за единицу времени t:
  
• если задан угол поворота φ за единицу времени:
  

• Количество оборотов за единицу времени [об/мин], [c -1 ].
• Угол поворота за единицу времени [рад/с].

Быстрота изменения угла φ (перемещения из положения П₁ в положение П₂) – это и есть угловая скорость:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

Приняв k как единичный орт положительного направления оси, получим:

Читайте также: Цилиндр значение из толкового словаря

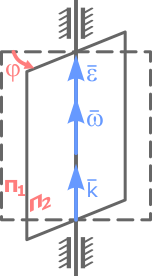
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Единицы измерения углового ускорения: [рад/с 2 ], [с -2 ]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает, а при отрицательном вращение замедляется.

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

равномерное вращение ( ω — const)

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Угловое ускорение

Система понятий кинематики включает в себя также такую величину как угловое ускорение тела. Дадим ей определение, рассмотрим основные аспекты с использованием примеров.

Видео:Урок 89 (осн). Задачи на вращательное движение - 1Скачать

Основные понятия

Угловое ускорение – величина, характеризующая изменение скорости с течением времени.

Пусть рассматриваемый промежуток времени это: Δ t = t 1 — t , а изменение угловой скорости составит Δ ω = ω 1 — ω , тогда числовое значение среднего углового ускорения за тот же интервал времени: » open=» ε = ∆ ω ∆ t = ε . Перейдем к пределу, когда Δ t > 0 , тогда формула углового ускорения будет иметь вид: ε = l i m ∆ t → 0 ∆ ω ∆ t = d ω d t = d 2 φ d t = ω ˙ = φ ¨ .

Числовое значение ускорения в заданный момент времени есть первая производная от угловой скорости или вторая производная от угла поворота по времени.

Размерность углового ускорения 1 T 2 (т.е. 1 в р е м я 2 ). Укажем также, в чем измеряется угловое ускорение: за единицу измерения стандартно принимается р а д / с 2 или иначе: 1 с 2 ( с — 2 ) .

Ускоренное вращение тела – это вращение, при котором угловая скорость (ее модуль) возрастает с течением времени.

Замедленное вращение тела – это вращение, при котором угловая скорость (ее модуль) убывает с течением времени.

В общем, довольно просто заметить, что, если ω и ε имеют одинаковые знаки, наблюдается ускоренное вращение, а, когда противоположные знаки – замедленное.

Рисунок 1 . Вектор углового ускорения

Если мы представим угловое ускорение как вектор ε → = d ω → d t , имеющий направление вдоль оси вращения, то в случае ускоренного вращения ε → и ω → совпадут по направлениям (левая часть
рисунка 1 ) и будут противоположны по направлениям в случае замедленного вращения (правая часть
рисунка 1 ).

Читайте также: Рабочий цилиндр сцепления форд транзит 2012 год

Видео:Урок 93. Основное уравнение динамики вращательного движенияСкачать

Закон равнопеременного вращения

Равнопеременное вращение – вращение, при котором угловое ускорение во все время движения является постоянным ( ε = c o n s t ) .

Выведем формульно закон равнопеременного вращения. Пусть в начальный момент времени t 0 угол вращения равен ϕ = ϕ 0 ; угловая скорость — ω = ω 0 (т.е. ω 0 является начальной угловой скоростью).

Выражение ε = d ω d t = ω ˙ = φ ¨ дает нам возможность сделать запись: d ω = ε d t . Проинтегрируем левую часть крайней записи в пределах от ω 0 до ω , а правую – в пределах от 0 до t , тогда:

ω = ω 0 + ε t , d φ = ω 0 d t + ε t d t .

Проинтегрируем вторично и получим формулу, выражающую закон равнопеременного вращения:

Закон равнопеременного вращения: φ = φ 0 + ω t + ε t 2 2 .

Вращение является равноускоренным, когда ω и ε имеют одинаковые знаки.

Вращение является равнозамедленным, когда ω и ε противоположны по знаку.

Угловое ускорение имеет связь с полным и тангенциальным ускорениями. Пусть некоторая точка вращается неравномерно по окружности с радиусом R , тогда: α r = ε R . Нормальное ускорение имеет также связь с угловым: a n = ω 2 R . Учтем это выражение и для полного ускорения получим: a = a r 2 + a n 2 = R ε 2 + ω 4 Для равнопеременного движения: ω = ε t ; a n = ω 2 R = ε 2 t 2 R и a = R ε 2 + ε 4 t 4 = R ε 1 + ε 2 t 4 .

Видео:Урок 96. Простейшие задачи на вращение твердого телаСкачать

Практические примеры

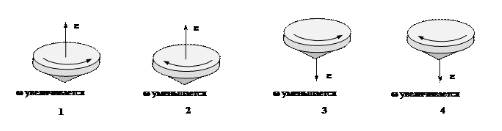
На рисунке 2 заданы различные типы вращения гироскопа (волчка). С учетом соответствующих подписей необходимо указать, какой рисунок верно демонстрирует направление углового ускорения.

Правило буравчика (правого винта) связывает направление вращения и псевдовектор угловой скорости. Рисунки 2 . 1 . и 2 . 3 . показывают направление псевдовектора вверх, а рисунки 2 . 2 . и 2 . 4 . – вниз.

Когда угловая скорость возрастает, ее приращение и вектор ускорения совпадут с вектором угловой скорости (рисунки 2 . 1 . и 2 . 4 . ). Когда угловая скорость будет уменьшаться, ее приращение и вектор ускорения окажутся противоположно направлены вектору угловой скорости (рисунки 2 . 2 . и 2 . 3 . ). Таким образом, все рисунки демонстрируют верное направление углового ускорения.

Пусть задана некоторая материальная точка, совершающая движение по окружности с радиусом R . При этом выражение ϕ = α t 3 отражает зависимость угла поворота от времени. Необходимо найти полное ускорение заданной точки как функцию времени.

Запишем выражения для угловой скорости и углового ускорения заданной точки:

ω = d φ d t = 3 α t 2 ; ε = 6 α t .

Полное ускорение запишем как:

a = a r 2 + a n 2 = R ε 2 + ω 4 = R 36 a 2 t 2 + 81 a 4 t 8 = 3 a t R 4 + 9 a 2 t 6 .

Видео:Момент инерции абсолютно твердого тела. Практическая часть. 10 класс.Скачать

Угловое ускорение

Угловое ускорение – это псевдовекторная физическая величина, которая равна первой производной от псевдовектора угловой скорости по времени:

Читайте также: Рабочий цилиндр сцепления suzuki liana

.

Угловое ускорение характеризует силу изменения модуля и направления угловой скорости при движении твердого тела.

Видео:Физика 10 класс (Урок№5 - Поступательное движение. Вращательное движение твердого тела.)Скачать

Ускорение точки твердого тела при свободном движении.

К понятию углового ускорения можно прийти, изучая определение ускорения точки твердого тела, находящегося в свободном движении. Определение скорости точки тела В (по формуле Эйлера) в свободном движении:

.

где — скорость точки тела А, которая была принята как полюс; — псевдовектор угловой скорости тела; — вектор, который был выпущен из полюса в точку – его скорость определяем. Продифференцировав это выражение по времени данное выражение, получаем:

.

где — является ускорением полюса А; — псевдовектором углового ускорения.

Составляющая ускорения точки В, которая определяется через угловое ускорение называется вращательным ускорением точки В около полюса А.

.

Последнее слагаемое в полученной формуле, которое зависит от угловой скорости, называется осестремительным ускорением точки В вокруг полюса А.

.

Видео:Вращательное движение. Практическая часть. 10 класс.Скачать

Угловое ускорение при вращении тела вокруг неподвижной оси.

Когда происходит вращение тела около неподвижной оси, которая проходит через недвижимые точки тела О₁ и О₂, производные орта оси вращения = 0:

.

Отсюда вектор углового ускорения вычисляется тривиально через вторую производную угла поворота

или .

где — это алгебраическая величина углового ускорения.

Здесь псевдовектор углового ускорения (и угловая скорость) идет по оси вращения тела. В случае наличия одинакового знака у первой и второй производной угла поворота:

,

значит, вектор углового ускорения и вектор угловой скорости имеют одинаковое направление и тело имеет ускоренное вращение. Иначе, при , векторы угловой скорости и углового ускорения имеют противоположные направления, а, значит, тело вращается замедленно.

В теормехе обычно вводится понятие угловой скорости и углового ускорения, когда рассматривается вращение тела вокруг не двигающейся оси. При чем, для решения задачи используют зависимость от времени угла поворота тела

Отсюда закон движения точки тела можно выразить натурально, как длина дуги окружности, которую прошла точка, совершая поворот тела от определенного исходного положения φ₀ = φ (t₀)

где R является расстоянием от точки до оси вращения.

Продифференцировав вышеуказанное выражение по времени, найдем алгебраическую скорость точки:

.

где является алгебраической величиной скорости угловой.

Через геометрическую сумму тангенциального и нормального ускорения можно выразить ускорение точки тела при вращении:

.

При этом тангенциальное ускорение выходит в виде производной от алгебраической скорости точки:

.

где является алгебраической величиной углового ускорения. А при помощи ниже приведенной формулы определим нормальное ускорение точки тела:

.

🎬 Видео

Поступательное и вращательное движенияСкачать

Физика. 10 класс. Задачи на вращательное движениеСкачать

Урок 90 (осн). Задачи на вращательное движение - 2Скачать

Урок 103. Задачи на вращение твердого тела (ч.2)Скачать