Задачи на вращательное движение тела

Цилиндр 1, масса которого m_ц=78 кг и диаметр d=24 см, может свободно вращаться около горизонтальной оси. На цилиндр намотана гибкая нить, имеющая на конце груз 2 массой m_гр=10 кг. Падая, груз разматывает нить и вращает цилиндр (рис. 269, а).

Определить угловое ускорение цилиндра, натяжение нити, кинетическую энергию груза A и цилиндра через t=4 сек после начала движения.

Массой нити и трением в оси цилиндра пренебречь.

Видео:Момент инерции абсолютно твердого тела. Практическая часть. 10 класс.Скачать

Решение (при помощи метода кинетостатики и уравнения основного закона динамики для вращающегося тела)

1. В задаче рассматриваются два связанных между собой тела: вращающийся цилиндр и поступательно двигающийся груз. Мысленно разрежем нить и изобразим оба тела с действующими на них силами отдельно друг от друга.

2. На рис. 269, б показан цилиндр, на который действует вращающий момент пары сил (T, T₁), созданной натяжением нити (сила T₂ приложена к подшипнику цилиндра, см. § 45):

Видео:Вращательное движение. 10 класс.Скачать

Решение 2 (при помощи закона кинетической энергии)

1. Второе решение начинается с того, чем заканчивается первое.

Через t=4 сек оба тела приобретают кинетическую энергию благодаря работе, произведенной грузом 2 при падении с высоты h (рис. 270).

6. Так как значение углового ускорения ε известно, легко найти величины кинетических энергий E_ц и E_гр (см. п. 2 решения).

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Как найти ускорение оси цилиндра

2017-05-21
На полый тонкостенный цилиндр массы $m$ намотана нить (тонкая и невесомая) (рис.). Свободный конец ее прикреплен к потолку лифта, движущегося вниз с ускорением $\vec_ $. Цилиндр предоставлен сам себе. Найти ускорение цилиндра относительно лифта и силу натяжения нити. Во время движения нить считать вертикальной.

В процессе движения цилиндр взаимодействует с Землей и с нитью. Благодаря этим взаимодействиям на цилиндр действуют сила тяжести $m \vec $, приложенная к центру масс и направленная вниз, и сила натяжения $\vec $ нити, направленная вдоль нити вверх. Сила эта создает вращающий момент относительно воображаемой оси, проходящей через центр масс и расположенной перпендикулярно плоскости рисунка. (Последнее утверждение справедливо в предположении, что силы $\vec $ и $m \vec $ находятся в одной вертикальной плоскости, перпендикулярной оси цилиндра.) Следовательно, цилиндр совершает сложное плоское движение — вращение вокруг указанной оси и поступательное движение. Поступательное движение цилиндра связано как с разматыванием нити, так и с движением лифта. Поскольку лифт движется ускоренно, система отсчета, связанная с лифтом, будет неинерциальной. В системе отсчета, связанной с Землей, уравнения движения цилиндра:

где $\vec $ — момент силы натяжения нити относительно горизонтальной оси, проходящей через центр цилиндра; $\vec_ $ — ускорение центра масс цилиндра относительно Земли. Очевидно,

где $\vec _ ^ $ — скорость центра масс цилиндра относительно лифта, т. е. скорость поступательного движения; $\vec_ $ — линейная скорость, обусловленная вращением, причем $u_ = \omega r$, где $\omega$ — угловая скорость, $r$ — радиус цилиндра. В точке А, принадлежащей одновременно и цилиндру, и вертикальной части нити, неподвижной относительно лифта, $v_^ = v_ ^ — u_ = 0$. Следовательно, $v_ ^ = \omega r$, откуда после дифференцирования по времени получим

Читайте также: Порядок работы цилиндров т 170

Для перехода к скалярным соотношениям введем оси Y и Z. В проекциях на эти оси

$a_ = a_ = a_ + a^ , \epsilon_ = \epsilon, M_ = Tr$.

Для полого цилиндра $J = mr^ $. Тогда векторные уравнения (1) можно записать в скалярном виде:

$m(a_ + a^ ) = mg — T, mr^ \epsilon = Tr$.

Решив эту систему с учетом соотношения (3), получим

Исследуя полученные выражения, легко видеть следующее:
1) если лифт свободно падает, т. е. $a_ = g$, то сила натяжения нити и относительное ускорение будут равны нулю; равенство $a^ = 0$ означает, что цилиндр будет двигаться только вместе с нитью (нет вращательного движения);
2) если ускорение лифта направлено вверх, т. е. $a_ $ центра масс цилиндра при этом уменьшается.

Видео:Вращательное движение твёрдого тела. Задачи 1, 2, 3Скачать

Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях – решение задачи

Видео:Урок 100. Задачи на вращение твердого тела (ч.1)Скачать

Основные законы и формулы, применяемые при решении задач

Вращательное движение вокруг неподвижной оси

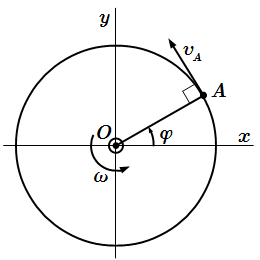
Рассмотри твердое тело, вращающееся вокруг неподвижной оси z . Сделаем рисунок. Ось вращения направим перпендикулярно плоскости рисунка, на нас. Пусть φ – угол поворота тела вокруг оси, отсчитываемый от некоторого начального положения. За положительное направление выберем направление против часовой стрелки. Угловая скорость ω равна производной угла поворота по времени t :
.
При , тело вращается против часовой стрелки; при – по часовой. Вектор угловой скорости направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

Угловое ускорение ε равно производной угловой скорости по времени:
.
Вектор углового ускорения также направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

Скорость точки при вращательном движении тела вокруг неподвижной оси

Рассмотрим точку A , принадлежащую твердому телу. Опустим из нее перпендикуляр OA на ось вращения. Пусть – расстояние от точки до оси. Траекторией движения точки A является окружность (или дуга) с центром в точке O радиуса .

Абсолютное значение скорости точки A определяется по формуле:
.
Вектор скорости направлен по касательной к траектории (окружности), перпендикулярно отрезку OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор угловой скорости .

Касательное (или тангенциальное) ускорение точки A определяется аналогично скорости:
.
Оно направлено по касательной к окружности, перпендикулярно OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор углового ускорения .

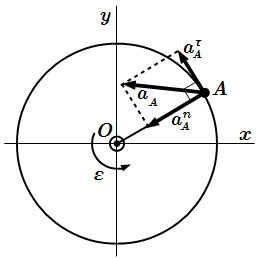
Ускорение точки при вращательном движении тела вокруг неподвижной оси

Нормальное ускорение всегда направлено к центру окружности и имеет абсолютную величину
.

Полное ускорение точки A , или просто ускорение, равно векторной сумме касательного и нормального ускорений:
.
Поскольку векторы и перпендикулярны, то абсолютная величина ускорения точки A определяется по формуле:
.

Поступательное прямолинейное движение

Теперь рассмотрим прямолинейное поступательное движение тела. Направим ось x вдоль его линии движения. Пусть s есть перемещение тела вдоль этой оси относительно некоторого начального положения. Тогда скорость движения всех точек тела равна производной перемещения по времени:
.
При , вектор скорости направлен вдоль оси x . При – противоположно этой оси.

Читайте также: Как определить количество цилиндров в жестком диске

Ускорение точек тела равно производной скорости по времени, или второй производной перемещения по времени:
.
При , вектор ускорения направлен вдоль оси x . При – противоположно.

Соприкосновение тел без проскальзывания

Рассмотрим два тела, находящиеся в зацеплении без проскальзывания. Пусть точка A принадлежит первому телу, а точка B – второму. И пусть, в рассматриваемый момент времени, положения этих точек совпадают. Тогда, если между телами нет проскальзывания, то скорости этих точек равны:
.
Если каждое из тел вращается вокруг неподвижной оси, то равны соответствующие касательные ускорения:
.
Если одно из тел движется поступательно (пусть это второе тело), то ускорение его точек равно касательному ускорению точки соприкосновения первого тела:
.

Видео:Вращательное движение. Практическая часть. 10 класс.Скачать

Пример решения задачи

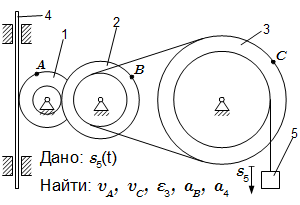
Механизм состоит из ступенчатых колес 1, 2, 3, находящихся в зацеплении и связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны соответственно: у колеса 1 – r₁ = 2 см, R₁ = 4 см, у колеса 2 – r₂ = 6 см, R₂ = 8 см, у колеса 3 – r₃ = 12 см, R₃ = 16 см. На ободьях колес расположены точки A, B и C. Задан закон движения груза: s₅ = t 3 – 6t (см). Положительное направление для s₅ – вниз.

Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.

Указания. Эта задача – на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что проскальзывание в ременной передаче и в точках сцепления колес отсутствует. То есть скорости точек колес, находящихся в зацеплении равны, а скорости точек ремня равны скорости точек, лежащих на ободе колес, связанных ременной передачей.

Дано:
t = 2 с; r₁ = 2 см, R₁ = 4 см; r₂ = 6 см, R₂ = 8 см; r₃ = 12 см, R₃ = 16 см; s₅ = t 3 – 6t (см).

Определение скорости и ускорения груза 5

Груз 5 совершает поступательное движение. Поэтому скорости (и ускорения) всех его точек равны. В условии задачи задано смещение s груза относительно некоторого начального положения. Дифференцируя по времени t , находим зависимость скорости точек груза от времени:
.
Дифференцируя скорость груза по времени, находим зависимость ускорения груза от времени:
.

Находим скорость и ускорение груза в заданный момент времени :
см/с;
см/с 2 .

Определение угловых скоростей и ускорений колес

Груз 5 связан нитью с внутренним ободом колеса 3. Поэтому скорости точек внутреннего обода колеса 3 равны скорости груза:
.
Отсюда находим угловую скорость колеса 3 для произвольного момента времени:
.
Здесь подразумевается, что и являются функциями от времени t . Дифференцируя по t , находим угловое ускорение колеса 3:
.
Находим значения угловой скорости и углового ускорения в момент времени с. Для этого подставляем найденные значения и при с:
с –1 ;
с –2 .

Рассмотрим колесо 2. Его внутренний обод связан нитью с внешним ободом колеса 3. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 2 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Рассмотрим колесо 1. Его внутренний обод находится в зацеплении с внешним ободом колеса 2. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 1 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Читайте также: Цилиндр mul t lock classic pro

Итак, мы нашли:
ω ₁ = 5.3333 с –1 , ω ₂ = 1.3333 с –1 , ω ₃ = 0.5 с –1 , ε ₁ = 10.6667 с –2 , ε ₂ = 2.6667 с –2 , ε ₃ = 1 с –2 .

Определение скоростей точек A и C

Точка A лежит на окружности радиуса R₁ с центром в точке O₁, расположенной на оси вращения. Поэтому скорость этой точки направлена по касательной к окружности и по абсолютной величине равна
см/с.

Точка C лежит на окружности радиуса R₃ с центром O₃ на оси вращения. Скорость этой точки:
см/с.

Определение ускорения точки B

Точка B лежит на окружности радиуса R₂ с центром O₂, расположенном на оси вращения. Касательное (или тангенциальное) ускорение этой точки направлено по касательной к окружности в сторону, на которую указывает угловое ускорение (по часовой стрелке). По абсолютной величине оно равно
см/с 2 .

Нормальное ускорение всегда направлено к центру окружности. По абсолютной величине оно равно
см/с 2 .

Полное ускорение равно векторной сумме касательного и нормального ускорений:
.
Поскольку касательное ускорение перпендикулярно нормальному, то для абсолютной величины полного ускорения имеем:
см/с 2 .

Определение ускорения рейки 4

Рейка 4 движется поступательно по направляющим. Она находится в зацеплении с внешним ободом колеса 1. Поэтому ее скорость равна скорости точек внешнего обода колеса 1:
.
Дифференцирую по времени, получаем ускорение рейки в произвольный момент времени:
.
Подставляем численные значения для момента времени t = 2 с :
см/с 2 .

см/с; см/с; с –2 ; см/с 2 ; см/с 2 .

Автор: Олег Одинцов . Опубликовано: 25-10-2019

Видео:Урок 96. Простейшие задачи на вращение твердого телаСкачать

Как найти ускорение оси цилиндра

2019-02-20
На наклонную плоскость, образующую угол а с горизонтом, поместили куб и тонкостенный цилиндр. Коэффициент трения между кубом и плоскостью равен $\mu$; коэффициент трения между цилиндром и плоскостью такой же. Ось цилиндра горизонтальна. Найдите ускорения, с которыми будут съезжать вниз куб и цилиндр и постройте графики зависимостей этих ускорений от $\mu$. При каких $\mu$ какая из фигур выиграет «гонку», если пустить тела по наклонной плоскости наперегонки (без начальной скорости)? Ускорение свободного падения $g$.

Проще всего найти ускорение куба. На наклонной плоскости на него действует сила тяжести $mg$, сила реакции опоры $N$ и сила, трения $F_ \leq \mu N$. Перпендикулярно плоскости силы скомпенсированы, $N = mg \cos \alpha$. Если куб скользит вниз, сила трения достигает предельного значения $F_ = \mu N = \mu mg \cos \alpha$. Проектируя все сины на направление движения, по второму закону Ньютона получаем

$ma_ = mg \sin \alpha — F_ , a_ = g( \sin \alpha — \mu \cos \alpha), \mu \leq tg \alpha$.

Последнее неравенство означает, что ускорение куба всегда положительно. Если же это условие не выполняется, равенство $F_ = \mu N$ превращается в неравенство $F_ tg \alpha/2$ — только в этом случае цилиндр скатывается без проскальзывания.

Если же качение осуществляется с проскальзыванием, в формулу (1) следует подставить предельное значение силы трения — силу трения скольжения gmg cos a, что дает ответ, совпадающий с ускорением куба.

Осталось лишь свести результаты для ускорений фигур в виде граифков и заметить, что при $\mu tg \alpha$ куб вообще не едет, значит, снова выиграет цилиндр.
Ответ: Зависимости ускорений тел от коэффициента трения представлены на графике, см. рис., черный — куб, серый — цилиндр. При малых ($\mu Источник

💡 Видео

Урок 89 (осн). Задачи на вращательное движение - 1Скачать

Физика 10 класс (Урок№5 - Поступательное движение. Вращательное движение твердого тела.)Скачать

Кинематика вращательного движения. ТермехСкачать

Поступательное и вращательное движенияСкачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Урок 93. Основное уравнение динамики вращательного движенияСкачать

Физика. 10 класс. Задачи на вращательное движениеСкачать

Урок 103. Задачи на вращение твердого тела (ч.2)Скачать

Поступательное и вращательное движения.Скачать