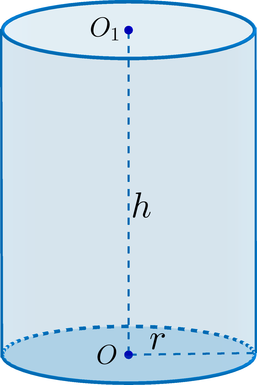
Даны два цилиндра. Радиус основания и высота первого равны соответственно 2 и 6, а второго — 6 и 7. Во сколько раз объём второго цилиндра больше объёма первого?
Объём цилиндра находится по формуле:
Найдём объём первого цилиндра:
Найдём объём второго цилиндра:
Найдём отношение объёма второго шара к первому:
Радиус основания цилиндра равен 26, а его образующая равна 9. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 24. Найдите площадь этого сечения.
Даны два цилиндра. Радиус основания и высота первого равны соответственно 4 и 18, а второго — 2 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?
Площадь боковой поверхности цилиндра находится по формуле:
Найдём площадь боковой поверхности первого цилиндра:
Найдём площадь боковой поверхности второго цилиндра:
Найдём отношение площади боковой поверхности цилиндра первого цилиндра ко второму:
Радиус основания цилиндра равен 13, а его образующая равна 18. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения.
Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно
Даны два шара с радиусами 9 и 3. Во сколько раз площадь поверхности большего шара больше площади поверхности меньшего?
Сечение, параллельное оси цилиндра, — прямоугольник. Одна его сторона равна образующей цилиндра. Найдем вторую его сторону из прямоугольного треугольника в основании по формуле: где AB — данная сторона, r — радиус основания цилиндра, аh — расстояние от сечения до оси цилиндра. Таким образом, площадь данного сечения равна 18 · 10 = 180.
В основании правильной четырехугольной пирамиды лежит квадрат. Где СH — половина его диагонали: а его площадь равна По теореме Пифагора находим высоту данной пирамиды Отсюда ее объем равен:
Площади шаров относятся как квадраты их радиусов, следовательно, площадь второго шара в раз больше площади первого.
Видео:Задания 11, 13 (часть 4) | ЕГЭ 2024 Математика (база) | Цилиндр, конусСкачать
Задачи для подготовке к ЕГЭ по теме: «Цилиндр. Площадь поверхности цилиндра»
Ищем педагогов в команду «Инфоурок»
Задачи для подготовки к ЕГЭ
» Цилиндр. Площадь поверхности цилиндра»
№ 1 Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на .
№2 Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
№ 3 Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на .
№4 Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
№5 Площадь боковой поверхности цилиндра равна 2 , а диаметр основания — 1. Найдите высоту цилиндра.
№6 Радиус основания цилиндра равен 26, а его образующая равна 9. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 24. Найдите площадь этого сечения.
№7 Даны два цилиндра. Радиус основания и высота первого равны соответственно 4 и 18, а второго — 2 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?
Читайте также: Цилиндр радиусом r расположенный вертикально
№1 Радиус основания цилиндра равен 7, высота равна 10. Найдите площадь боковой поверхности цилиндра, деленную на .
№2 Длина окружности основания цилиндра равна 3, высота равна 4. Найдите площадь боковой поверхности цилиндра.
№3 Площадь осевого сечения цилиндра равна 7. Найдите площадь боковой поверхности цилиндра, деленную на .
№4 Длина окружности основания цилиндра равна 14. Площадь боковой поверхности равна 182. Найдите высоту цилиндра.
№5 Площадь боковой поверхности цилиндра равна 21, а диаметр основания равен 7. Найдите высоту цилиндра.
№6 Радиус основания цилиндра равен 13, а его образующая равна 18. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения.
№7 Даны два цилиндра. Радиус основания и высота первого равны соответственно 2 и 3, а второго — 12 и 5. Во сколько раз площадь боковой поверхности второго цилиндра больше площади боковой поверхности первого?
Видео:ЕГЭ по математике. Базовый уровень. Задание 13. Объем цилиндра.Скачать
Задания с цилиндром базовый
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Если сначала найти объем целого цилиндра, то он равен 1/3 * ПИ * r^2 * H, где r=6, H=5, то есть объем цилиндра равен 60 пи, а потом разделить его на четыре, т.к. данный сектор занимает 1/4 части всего цилиндра, то получится 15. В чем дело, что не так?
Ошибка в формуле. Объём цилинлра равен произведению высоты на площадь основания.
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной фигуры равен сумме объемов цилиндра с радиусом основания 2 и высотой 3 и половины цилиндра с тем же радиусом основания и высотой 1:
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной фигуры равен сумме объемов цилиндра с радиусом основания 2 и высотой 3 и половины цилиндра с тем же радиусом основания и высотой 1:
Добрый день,в условии указано что первая высота равна 3, а вторая 1. Почему в решении написано 0,5H(2)?
Читайте также: Рулевой цилиндр лиаз 5256
Так учитывается половина цилиндра
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной фигуры равен разности объемов цилиндра с радиусом основания 5 и высотой 5 и цилиндра с той же высотой и радиусом основания 2:
Видео:ВСЯ СТЕРЕОМЕТРИЯ НА БАЗОВЫЙ ЕГЭ-2024 // КОНЦЕНТРАТ // МАТЕМАТИКАСкачать
Задачи на тему «Цилиндр»
\(\blacktriangleright\) Ось цилиндра – прямая, соединяющая центры его оснований.
Отрезок, соединяющий центры оснований – высота.
\(\blacktriangleright\) Образующая цилиндра – перпендикуляр, проведенный из точки границы одного основания к другому основанию.
Заметим, что образующая и высота цилиндра равны друг другу.
\(\blacktriangleright\) Площадь боковой поверхности цилиндра \( >=2\pi rh>>\) , где \(r\) – радиус основания, \(h\) – высота (или образующая).
\(\blacktriangleright\) Площадь полной поверхности цилиндра равна сумме площади боковой поверхности и площадей оснований. \[ >=2\pi rh+2\pi r^2>>\]
\(\blacktriangleright\) Объем цилиндра \( >\cdot h=\pi r^2h>>\)
Заметим, что прямой цилиндр имеет некоторое сходство с прямой призмой, только в ее основаниях лежат многоугольники (граница которых – ломаная), а в основаниях цилиндра – круги (граница которых гладкая).
Поэтому можно сказать, что боковая поверхность прямой призмы “ребристая”, а цилиндра – “гладкая”.
Про прямые круговые цилиндры \(C_1\) и \(C_2\) известно, что у \(C_1\) радиус основания в два раза больше, чем у \(C_2\) , но у \(C_2\) высота в три раза больше, чем у \(C_1\) . Найдите отношение объёма цилиндра \(C_2\) к объёму \(C_1\) .
Обозначим высоту цилиндра \(C_1\) через \(h_1\) , а высоту цилиндра \(C_2\) через \(h_2\) . Обозначим радиус основания цилиндра \(C_1\) через \(r_1\) , а радиус основания цилиндра \(C_2\) через \(r_2\) . Тогда \[r_1 = 2r_2,\qquad h_2 = 3h_1\,.\]
Объём цилиндра \(C_1\) равен \(\pi ^2 h_1 = 4\pi ^2 h_1\) , а объём цилиндра \(C_2\) равен \(3\pi ^2 h_1\) , тогда \[\dfrac > > = \dfrac ^2 h_1> ^2 h_1> = 0,75\]
Объем цилиндра равен \(64\pi\) , а площадь боковой поверхности равна \(32\pi\) . Найдите площадь полной поверхности цилиндра, деленную на \(\pi\) .
Формулы для нахождения объема и боковой поверхности цилиндра: \(V = \pi R^2 h\) , \(S_ > = 2\pi R h\) . Зная величину объема и боковой поверхности, можно выразить радиус цилиндра: \[\frac >> = \frac = \frac = \frac = 2\] \(\Rightarrow\) \(R = 4\) . Площадь полной поверхности складывается из площади боковой поверхности и площадей двух оснований: \[S_ > = 2\pi R h + 2 \pi R^2 = 32\pi + 2 \cdot 16\pi = 64\pi.\] Осталось разделить полученный объем на \(\pi\) , тогда окончательно получаем \(64\) .
Объем цилиндра равен \(100\pi\) , а площадь боковой поверхности равна \(25\pi\) . Найдите высоту цилиндра.
Формулы для нахождения объема и боковой поверхности цилиндра: \(V = \pi R^2 h\) , \(S_ > = 2\pi R h\) . Зная величину объема и боковой поверхности, можно выразить радиус цилиндра: \[\frac >> = \frac = \frac = \frac = 4\] \(\Rightarrow\) \(R = 8\) . Подставим значение радиуса в формулу объема и найдем из этой формулы искомую высоту: \[V = \pi R^2 h = 64\pi h = 100\pi\] \(\Rightarrow\) \(\displaystyle h = \frac = 1,5625\) .
Объём цилиндра \[V = \dfrac >,\] а отношение радиуса его основания к его высоте равно \(5\) . Найдите площадь полной поверхности этого цилиндра.
\[V_ > = \pi R^2 H = \dfrac >,\] \(\dfrac = 5\) , где \(R\) – радиус основания цилиндра, \(H\) – его высота, тогда \(R = 5H\) , следовательно, \[\pi \cdot 25 H^3 = \dfrac >\qquad\Rightarrow\qquad H^3 = \dfrac >,\] откуда \(H = \dfrac >\) , \(R = \dfrac >\) . \[S_ > = 2\pi R H + \pi R^2 = 2\pi R(H + R) = 2\pi\cdot\dfrac >\cdot\dfrac > = 240.\]
Читайте также: Рабочий цилиндр сцепления patriot
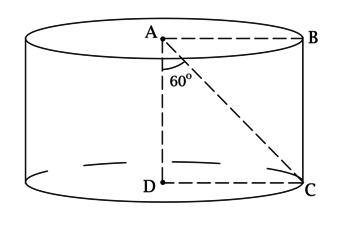
\(AD\) – ось цилиндра, \(BC\) – его образующая, \(S_ = \dfrac > >\) , \(\angle CAD = 60^\circ\) . Найдите объём цилиндра.
Так как \(AD\) и \(BC\) – высоты цилиндра, то \(ABCD\) – прямоугольник, тогда \[S_ = AD\cdot DC = H\cdot R = \dfrac > >.\]
Рассмотрим прямоугольный треугольник \(ADC\) :
Т.к. \(\angle DAC = 60^\circ\) , то \[AD = \mathrm \, \angle ACD\cdot DC = \mathrm \, 30^\circ\cdot R = \dfrac >,\] т.е. \(H = \dfrac >\) или \(R = \sqrt H\) .
Повторение базовой теории и формул, в том числе и тех, которые позволяют выполнить расчет объема цилиндра, — один из основных этапов подготовки к ЕГЭ. Несмотря на то, что эта тема достаточно подробно рассматривается на уроках математики в школе, с необходимостью вспомнить основной материал и «прокачать» навык решения задач сталкиваются многие учащиеся. Понимая, как вычислить объем и другие неизвестные параметры цилиндра, старшеклассники смогут получить достаточно высокие баллы по итогам сдачи единого государственного экзамена.
Видео:Видеоурок по математике "Цилиндр"Скачать
Основные нюансы, которые стоит вспомнить
Чтобы вопрос, как посчитать объем цилиндра и выполнить измерение других неизвестных параметров при решении задач, не ставил ученика в тупик, рекомендуем повторить основные свойства этой фигуры прямо сейчас в режиме онлайн.
- Цилиндр представляет собой тело, которое ограничено цилиндрической поверхностью и двумя кругами. Цилиндрическая поверхность является боковой. А круги представляют собой основания фигуры.
- Высота цилиндра есть расстояние между плоскостями его оснований.
- Все его образующие являются параллельными и равными между собой.
- Радиус цилиндра есть радиус его основания.
- Фигура называется прямой, если ее образующие перпендикулярны основаниям.
Видео:ЕГЭ Базовая Математика | Объемы: 11 и 13 заданиеСкачать
Как подготовиться к экзамену качественно и эффективно?
Занимаясь накануне прохождения аттестационного испытания, многие учащиеся сталкиваются с проблемой поиска необходимой информации. Далеко не всегда школьный учебник оказывается под рукой, когда это требуется. А найти формулы, которые помогут рассчитать площадь и другие неизвестные параметры цилиндра, часто бывает достаточно сложно даже в Интернете в онлайн-режиме.
Занимаясь вместе с математическим порталом «Школково», выпускники смогут избежать типовых ошибок и успешно сдать единый госэкзамен. Мы предлагаем выстроить процесс подготовки по-новому, переходя от простого к сложному. Это позволит учащимся определить непонятные для себя тематики и ликвидировать пробелы в знаниях.
Весь базовый материал, который поможет в решении задач на тему «Цилиндр», выпускники смогут найти в разделе «Теоретическая справка». Специалисты «Школково» изложили с доступной форме все необходимые определения и формулы.
Для закрепления полученных знаний учащиеся могут попрактиковаться в решении задач на тему «Цилиндр» и другие темы, например, нахождение площади или объема конуса. Большая, постоянно обновляющаяся подборка заданий представлена в разделе «Каталог».
Чтобы во время подготовки к ЕГЭ быстро найти конкретную задачу по теме «Цилиндр» и освежить в памяти алгоритм ее решения, выпускники могут предварительно сохранить ее в «Избранное». Отрабатывать собственные навыки на нашем сайте имеют возможность не только столичные школьники, но и учащиеся из других российских городов.
📺 Видео
Задача про ЦИЛИНДР / Как найти объем детали? / Профиль ЕГЭСкачать
Цилиндр, конус и шар в задании 2 | Математика ЕГЭ 2023 | УмскулСкачать
РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать
🔴 В бак, имеющий форму цилиндра, налито ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
Как решить ЕГЭ по математике (база): 7, 16, 17 задания | Решу ЕГЭ за 10 минутСкачать
Объем цилиндра. Практическая часть. 11 класс.Скачать
✓ Задача про цилиндр | ЕГЭ-2018. Задание 14. Математика. Профильный уровень | Борис ТрушинСкачать
Задания 11, 13 (часть 1) | ЕГЭ 2024 Математика (база) | Куб, прямоугольный параллелепипедСкачать
ЦИЛИНДР. КОНУС. ШАР. ЕГЭ. ЗАДАНИЕ 5.СТЕРЕОМЕТРИЯСкачать
Стереометрия все типы. 3 задание егэ по математике профильСкачать
ЗАДАНИЕ 19 С РЕАЛЬНОГО ЕГЭ | Как найти неизвестное число | Базовая математика УмскулСкачать
ЕГЭ по математике. Базовый уровень. Задание 16. Цилиндр. Площадь прямоугольника.Скачать
🔴 Даны две кружки цилиндрической формы ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
ЕГЭ. Математика. База . Задача 16. Радиус основания цилиндра равен 26.Скачать
Стереометрия 3 задание. ЕГЭ по математике 2024 | Аня МатеманяСкачать
