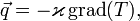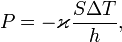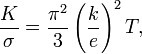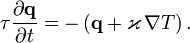- Постановка задачи и вывод дифференциального уравнения теплопроводности для сплошного цилиндра. Аналитическое решение.
- Закон Фурье – основной закон теплопроводности.
- Закон Фурье
- Коэффициенты теплопроводности различных веществ
- Коэффициент теплопроводности вакуума
- Связь с электропроводностью
- Обобщения закона Фурье
- 🎥 Видео
Видео:Интуитивное понимание формулы теплопроводности (часть 11) | Термодинамика | ФизикаСкачать

Постановка задачи и вывод дифференциального уравнения теплопроводности для сплошного цилиндра. Аналитическое решение.
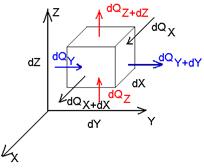
Дифференциальное уравнение теплопроводности выводится на основе закона сохранения энергии. Из всего рассматриваемого объема выделим элементарный объем dV и процесс будем рассматривать в течении элементарного промежутка времени.
· Тепло физические параметры среды постоянны
· Температурной деформацией пренебрегаем
· Внутренний источник тепла , если он есть, распределен по всему объему
dQ1 – количество тепла подведенного к рассматриваемому объему dV за время dτ за счет процессов электропроводности
dQ2 – количество тепловой энергии, которой выделяется на dV за dτ за счет действия внутреннего источника тепла
dQ – изменение внутренней энергии рассматриваемого объема за dτ (изменение энтальпии тела).
Ø Методы переноса тепла: теплопроводность, тепловая конвекция, излучение
Ø Конвективный обмен – возможен только в подвижных средах. Перенос осуществляется только за счет перемещение самого вещества.
Ø Тепловое излучение – перенос тепла происходит в 2 этапа. Сначала тепло преобразуется в тепловую энергию, а затем обратно.
Ø Теплопроводность – перенос тепла в твердых телах, жидкостях или газах, если жидкость и газы неподвижны.
Механизм данного явления объясняется на основании молекулярно — кинетических изменений. Перенос энергии осуществляется вследствие теплового движения и энергетического взаимодействия между микрочастицами (молекулами, атомами, электронами), из которых состоит данное тело.
Теплопроводность в чистом виде существует только в твердых телах. А в подвижных средах теплообмен осуществляется за счет теплопроводности, конвекции и излучения.
По теплопроводности тепло распространяется от нагретых участков к холодным, то есть в сторону убывания температуры.
Температура определяет степень нагретости тела.
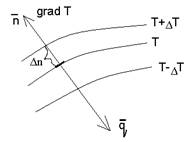
Процесс теплопроводности неразрывно связан с распределением температуры внутри тела, поэтому необходимо дать определение температурному полю и градиенту температуры:
— температурным полем называется совокупность значений температуры в каждой точке пространства в данный момент времени
Геометрическое место точек в пространстве имеющих одинаковую температуру, называется изотермической поверхностью
Поскольку любая точка пространства в данный момент времени может иметь только одно значение температуры, то изотермические поверхности не пересекаются →
— температурный градиент – предел отношения изменения температуры ΔТ к расстоянию между изотермами по нормали Δn.
Lim (ΔТ / Δn) Δn→0 = = grad T. -единичный вектор
Является вектором, направленным по нормали к изотермической поверхности в сторону возрастания температуры его размерность [ 0 С/м]
Наибольшее изменение температуры может происходить по нормали к изотермическим поверхностям.
· Количества тепла, прошедшего через произвольную изотермическую поверхность за некоторый интервал времени τ – будем обозначать P [Вт]
· Количества тепла, прошедшего через произвольный изотермическую поверхность в единицу времени будем обозначать – тепловой поток Q [Дж].
Читайте также: В цилиндре площадь основания которого равна 100 см2
· Тепловой поток отнесенный к единице поверхности, называется плотностью теплового потока – q [Вт/м 2 ]
· Закон Фурье (связь q и grad T). Фурье экспериментально установил что, количество переданного тепла пропорционально падению температуры, времени и площади сечения, перпендикулярного направлению распространению тепла
· λ – коэффициент теплопроводности – представляет собой количество тепла, которое роходит в единицу времени через один квадратный метр изотремической поверхности при температурном градиенте =1
В общем случаи λ зависит от температуры
· С – теплоемкость – количество энергии необходимого для нагрева 1 кг вещества на 1 градус. [Дж/кг 0 С]
dQX = qX * dY * dZ * dτ
dQ2 = qV dV dτ, где qV – количества тепла выделившегося в единице объема в единицу времени (внутренний источник тепла).
dQ = dU = ρ C dV dτ , где ρ – плотность среды [кг/м 3 ]
Из закона Фурье:
а – коэффициент температура проводность [м 2 / 0 С]
Постановка задачи:
1. рассматриваем сплошной цилиндр
3. цилиндрическая система координат
4. теплофизические свойства постоянны
5. внутреннего источника тепла нет (qV =0)
Переходим от декартовой системы координат к цилиндрической:
| Цилиндрические (Ц) и декартовые (Д) координаты связаны следующим образом: | |
| Д ® Ц | Ц ® Д |
Оператор Лапласа для цилиндрической системы координат запишется:
С учетом поставленной задачи получаем:
Охлаждение (нагревание) бесконечного длинного цилиндра.
Цилиндр радиусом г0 отдает теплоту окружающей среде через свою боковую поверхность; коэффициент теплоотдачи α во всех точках поверхности одинаков и остается постоянным на протяжении всего периода охлаждения. Температура среды Tcp постоянна. В начальный момент времени при τ = 0 температура является некоторой функцией T (r, 0) = f (r). При этих условиях уравнение теплопроводности принимает вид:
Граничные и начальные условия:
· при τ = 0 и 0 0 и r = 0
· при τ > 0 и r = r0
Сформулированную задачу решим с помощью разделения переменных, т. е.
(r, τ) = φ (τ) ψ (r).
Подставив это выражение в уравнение (*),получим два обыкновенных дифференциальных уравнения вида
Если обозначить kr0 = μ , тогда частное решение уравнения (*) будет иметь вид:
где — коэффициент температуро-проводность
Постоянная μ определяется из граничных условий (r= r0), решение которых приводит к характеристическому уравнению:
(2) где J1, (μ) — функция Бесселя первого рода первого порядка.
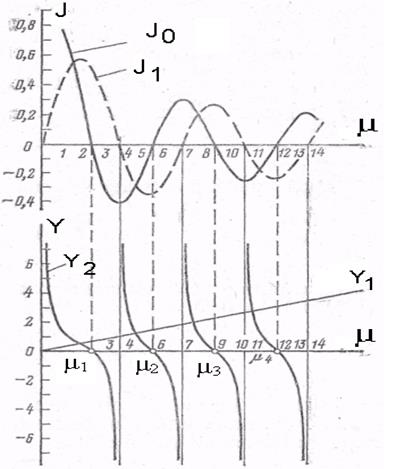
Уравнение (+) является трансцендентным, и его удобно решать графическим способом, обозначив:
· Отметим, что у2 обращается в нуль в тех точках, для которых Jo (μ) = 0.
· В тех точках, в которых функция J1 (μ1) обращается в нуль, функция у2 претерпевает разрыв непрерывности и становится равной ± оо.
Функции Jo (μ) и J1 (μ) являются периодическими затухающими функциями.
Читайте также: Цилиндры для автомобильных замков
— Кривая у2 = напоминает котангенсоиду, но с убывающим периодом.
— Функция у1 графически представляет прямую линию, проходящую через начало координат.
Выполнив построение, как показано на рис, в точках пересечения функции у2 с прямой у1 получим значения корней характеристического уравнения
Из рис следует, что уравнение (2) имеет бесчисленное множество решений, а сами корни, представляют ряд возрастающих чисел, т. е. μ1 100) прямая совпадает с осью абсцисс и корни характеристического уравнения не зависят от Bi, а определяются из условий
· Если рассматривать охлаждение цилиндра при условии Bi → 0
· Если Fo ≥ 0,25, при вычислении безразмерной температуры можно ограничиться первым членом ряда. Допускаемая при этом ошибка не превысит 1 %.
Дата добавления: 2016-04-19 ; просмотров: 2674 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:ЗАЧЕМ в жизни нужно преобразование Фурье? В Первом Приближении. Чуть-Чуть о Науке #НаукаСкачать

Закон Фурье – основной закон теплопроводности.
В 1807 году французский ученый Фурье доказал экспериментально, что во всякой точке тела (вещества) в процессе теплопроводности присуща однозначная взаимосвязь между тепловым потоком и градиентом температуры:
,
где Q – тепловой поток, выражается в Вт;
grad(T) – градиент температурного поля (совокупности числовых значений температуры в разнообразных местах системы в выбранный момент времени), единицы измерения К/м;
S – площадь поверхности теплообмена, м 2 ;
Градиент температуры получится характеризовать в виде векторной суммы составляющих по осям декартовых координат:
,
где i, j, k – ортогональные между собой единичные векторы, нацеленные по координатным осям.
Значит, данный закон устанавливает величину теплового потока при переносе тепла посредством теплопроводности.
Закон Фурье для поверхностной плотности теплового потока принимает вид:
.
Знак « минус» обозначает, что векторы теплового потока и градиента температуры разнонаправленные. Следует понимать, что теплота передается в направлении спада температуры.
И все же не лишним будет указать, что закон Фурье не принимает в расчет инерционность процесса теплопроводности, иначе говоря, в представленной модели колебание температуры в любой точке мгновенно распространяется на всё тело. Закон Фурье некорректно применять для характеристики высокочастотных процессов таких как, к примеру, распространение ультразвука, ударной волны.
Видео:AGalilov: Преобразование Фурье "на пальцах"Скачать
Закон Фурье
Теплопрово́дность — это перенос теплоты структурными частицами вещества (молекулами, атомами, электронами) в процессе их теплового движения. Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. Явление теплопроводности заключается в том, что кинетическая энергия атомов и молекул, которая определяет температуру тела, передаётся другому телу при их взаимодействии или передаётся из более нагретых областей тела к менее нагретым областям. Иногда теплопроводностью называется также количественная оценка способности конкретного вещества проводить тепло.
Исторически считалось, что передача тепловой энергии связана с перетеканием теплорода от одного тела к другому. Однако более поздние опыты, в частности, нагрев пушечных стволов при сверлении, опровергли реальность существования теплорода как самостоятельного вида материи. Соответственно, в настоящее время считается, что явление теплопроводности обусловлено стремлением занять состояние более близкое к термодинамическому равновесию, что выражается в выравнивании температуры.
Читайте также: Зеркальный цилиндр что это
В установившемся режиме поток энергии, передающейся посредством теплопроводности, пропорционален градиенту температуры:
где 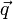
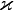
В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):
где P — полная мощность тепловых потерь, S — площадь сечения параллелепипеда, ΔT — перепад температур граней, h — длина параллелепипеда, то есть расстояние между гранями.
Коэффициент теплопроводности измеряется в Вт/(м·K).
Видео:ТеплопроводностьСкачать

Коэффициенты теплопроводности различных веществ
| Материал | Теплопроводность, Вт/(м·K) |
|---|---|
| Алмаз | 1001—2600 |
| Серебро | 430 |
| Медь | 382—390 |
| Золото | 320 |
| Алюминий | 202—236 |
| Латунь | 97—111 |
| Железо | 92 |
| Платина | 70 |
| Олово | 67 |
| Сталь | 47 |
| Кварц | 8 |
| Стекло | 1 |
| Вода | 0,6 |
| Кирпич строительный | 0,2—0,7 |
| Пенобетон | 0,14—0,3 |
| Газобетон | 0,1—0,3 |
| Дерево | 0,15 |
| Шерсть | 0,05 |
| Минеральная вата | 0,045 |
| Пенополистирол | 0,04 |
| Пеноизол | 0,035 |
| Воздух (300 K, 100 кПа) | 0,026 |
| Воздух (сухой неподвижный) | 0,024—0,031 |
| Аргон | 0,0177 |
| Ксенон | 0,0057 |
| Аэрогель | 0,003 |
| Вакуум (абсолютный) | 0 (строго) |
На практике нужно также учитывать проводимость тепла за счет конвекции молекул и проникаемости излучений. Например, при полной нетеплопроводности вакуума, тепло может передаваться за счет излучения (пример — Солнце, установки инфракрасного излучения). А газ или жидкость могут обмениваться нагретыми или охлажденными слоями самостоятельно или искусственно (пример — фен, греющие вентиляторы).
Видео:ТеплопроводностьСкачать

Коэффициент теплопроводности вакуума
Коэффициент теплопроводности вакуума стремится к нулю. Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тепло в вакууме передаётся только излучением. Поэтому для уменьшения теплопотери стенки термоса делают двойными, серебрят (такая поверхность хуже излучает и лучше отражает), а воздух между ними откачивают.
Видео:Учебный фильм - ТеплообменСкачать

Связь с электропроводностью
Связь коэффициента теплопроводности K с удельной электрической проводимостью σ в металлах устанавливает закон Видемана — Франца:
Видео:Л1 - Теплопроводность. Закон Фурье.Скачать

Обобщения закона Фурье
Следует отметить, что закон Фурье не учитывает инерционность процесса теплопроводности, то есть в данной модели изменение температуры в какой-то точке мгновенно распространяется на всё тело. Закон Фурье не применим для описания высокочастотных процессов (и, соответственно, процессов, чьё разложение в ряд Фурье имеет значительные высокочастотные гармоники). Примерами таких процессов являются распространение ультразвука, ударные волны и т. д. Инерционность в уравнения переноса первым ввел Максвелл [1] , а в 1948 году Каттанео был предложен вариант закона Фурье с релаксационным членом: [2]
Если время релаксации τ пренебрежимо мало, то это уравнение переходит в закон Фурье.
🎥 Видео
Закон БернуллиСкачать

С1 - Расчёт теплопроводности в твёрдых телах.Скачать

Теплопроводность цилиндрической стенкиСкачать

Уравнение, которое меняет взгляд на мир [Veritasium]Скачать
![Уравнение, которое меняет взгляд на мир [Veritasium]](https://i.ytimg.com/vi/DH1cv0Rdf2w/0.jpg)
Основы теплотехники. Второй закон термодинамики. Энтропия. Теорема Нернста.Скачать

Походная фляга или закон КирхгофаСкачать

Лекция 3.4 Теплопроводность. Основные понятия теплопроводности Закон Фурье.Скачать

Закон диффузии ФикаСкачать

Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

Теплопроводность плоской стенкиСкачать

Закон и уравнение теплопроводностиСкачать