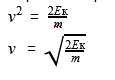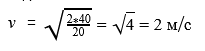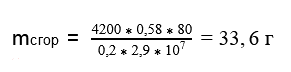Если мы погуглим определение слова «Энергия», то скорее всего найдем что-то про формы взаимодействия материи. Это верно, но совершенно непонятно.
Поэтому давайте условимся здесь и сейчас, что энергия — это запас, который пойдет на совершение работы.
Энергия бывает разных видов: механическая, электрическая, внутренняя, гравитационная и так далее. Измеряется она в Джоулях (Дж) и чаще всего обозначается буквой E.
- Механическая энергия
- Кинетическая энергия
- Потенциальная энергия
- Закон сохранения энергии
- Переход механической энергии во внутреннюю
- Закон сохранения энергии в тепловых процессах
- Закон сохранения энергии для цилиндра
- Основные законы и формулы
- Примеры решения задач
- Задачи для самостоятельного решения
- Качественные задачи
- Контрольные вопросы
- 📽️ Видео
Видео:Галилео. Эксперимент. Закон сохранения энергииСкачать

Механическая энергия
Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.
Она представляет собой совокупность кинетической и потенциальной энергии. Кинетическая энергия — это энергия действия. Потенциальная — ожидания действия.
Представьте, что вы взяли в руки канцелярскую резинку, растянули ее и отпустили. Из растянутого положения резинка просто «полетит», как только вы ей позволите это сделать. В этом процессе в момент натяжения резинка обладает потенциальной энергией, а в момент полета — кинетической.
Еще один примерчик: лыжник скатывается с горы. В самом начале — на вершине — у него максимальная потенциальная энергия, потому что он в режиме ожидания действия (ждущий режим ?), а внизу горы он уже явно двигается, а не ждет, когда с ним это случится — получается, внизу горы кинетическая энергия.
Кинетическая энергия
Еще разок: кинетическая энергия — это энергия действия. Величина, которая очевиднее всего характеризует действие — это скорость. Соответственно, в формуле кинетической энергии точно должна присутствовать скорость.
Кинетическая энергия
Ек — кинетическая энергия [Дж]
Чем быстрее движется тело, тем больше его кинетическая энергия. И наоборот — чем медленнее, тем меньше кинетическая энергия.
Задачка раз
Определить кинетическую энергию собаченьки массой 10 килограмм, если она бежала за мячом с постоянной скоростью 2 м/с.
Формула кинетической энергии Ек = (m*v^2)/2
Ответ: кинетическая энергия пёсы равна 20 Дж.
Задачка два
Найти скорость бегущего по опушке гнома, если его масса равна 20 килограммам, а его кинетическая энергия — 40 Дж
Формула кинетической энергии Ек = (m*v^2)/2
Ответ: гном бежал со скоростью 2 м/с.
Потенциальная энергия
В отличие от кинетической энергии, потенциальная чаще всего тем меньше, чем скорость больше. Потенциальная энергия — это энергия ожидания действия.
Например, потенциальная энергия у сжатой пружины будет очень велика, потому что такая конструкция может привести к действию, а следовательно — к увеличению кинетической энергии. То же самое происходит, если тело поднять на высоту. Чем выше мы поднимаем тело, тем больше его потенциальная энергия.
Потенциальная энергия деформированной пружины
Еп — потенциальная энергия [Дж]
Потенциальная энергия
Еп — потенциальная энергия [Дж]
g — ускорение свободного падения [м/с^2]
На планете Земля g ≃ 9,8 м/с^2
Задачка раз
Найти потенциальную энергию рака массой 0,1 кг, который свистит на горе высотой 2500 метров. Ускорение свободного падения считать равным 9,8 м/с^2.
Формула потенциальной энергии Еп = mgh
Ответ: потенциальная энергия рака, свистящего на горе, равна 2450 Дж.
Задачка два
Найти высоту горки, с которой собирается скатиться лыжник массой 65 килограмм, если его потенциальная энергия равна 637 кДж. Ускорение свободного падения считать равным 9,8 м/с^2.
Формула потенциальной энергии Еп = mgh
Переведем 637 кДж в Джоули.
Ответ: высота горы равна 1000 метров.
Задачка три
Два шара разной массы подняты на разную высоту относительно поверхности стола (см. рисунок). Сравните значения потенциальной энергии шаров E1 и E2. Считать, что потенциальная энергия отсчитывается от уровня крышки стола.
Потенциальная энергия вычисляется по формуле: E = mgh
Таким образом, получим, что
Ответ: E1 = E2.
Видео:Проверка закона сохранения и превращения механической энергии #ФизиканскиеЛьвы2018Скачать

Закон сохранения энергии
В физике и правда ничего не исчезает бесследно. Чтобы это как-то выразить, используют законы сохранения. В случае с энергией — Закон сохранения энергии.
Закон сохранения энергии
Полная механическая энергия замкнутой системы остается постоянной.
Полная механическая энергия — это сумма кинетической и потенциальной энергий. Математически этот закон описывается так:
Закон сохранения энергии
Еполн.мех. = Еп + Eк = const
Еполн.мех. — полная механическая энергия системы [Дж]
Еп — потенциальная энергия [Дж]
Ек — кинетическая энергия [Дж]
const — постоянная величина
Задачка раз
Мяч бросают вертикально вверх с поверхности Земли. Сопротивление воздуха пренебрежимо мало. Как изменится высота подъёма мяча при увеличении начальной скорости мяча в 2 раза?
Должен выполняться закон сохранения энергии:
В начальный момент времени высота равна нулю, значит Еп = 0. В этот же момент времени Ек максимальна.
В конечный момент времени все наоборот — кинетическая энергия равна нулю, так как мяч уже не может лететь выше, а вот потенциальная максимальна, так как мяч докинули до максимальной высоты.
Это можно описать соотношением:
Разделим на массу левую и правую часть
Из соотношения видно, что высота прямо пропорциональна квадрату начальной скорости, значит при увеличении начальной скорости мяча в два раза, высота должна увеличиться в 4 раза.
Ответ: высота увеличится в 4 раза
Задачка два
Тело массой m, брошенное с поверхности земли вертикально вверх с начальной скоростью v0, поднялось на максимальную высоту h0. Сопротивление воздуха пренебрежимо мало. Чему будет равна полная механическая энергия тела на некоторой промежуточной высоте h?
По закону сохранения энергии полная механическая энергия изолированной системы остаётся постоянной. В максимальной точке подъёма скорость тела равна нулю, а значит, оно будет обладать исключительно потенциальной энергией Емех = Еп = mgh0.
Таким образом, на некоторой промежуточной высоте h, тело будет обладать и кинетической и потенциальной энергией, но их сумма будет иметь значение Емех = mgh0.
Ответ: Емех = mgh0.
Задачка три
Читайте также: Клапан обратный 1 цилиндр компрессора 010249 d
Мяч массой 100 г бросили вертикально вверх с поверхности земли с начальной скоростью 6 м/с. На какой высоте относительно земли мяч имел скорость 2 м/с? Сопротивлением воздуха пренебречь.
Переведем массу из граммов в килограммы:
У поверхности земли полная механическая энергия мяча равна его кинетической энергии:
Е = Ек0 = (m*v^2)/2 = (0,1*6^2)/2 = 1,8 Дж
На высоте h потенциальная энергия мяча есть разность полной механической энергии и кинетической энергии:
mgh = E — (m*v^2)/2 = 1,8 — (0,1 * 2^2)/2 = 1,6 Дж
Ответ: мяч имел скорость 2 м/с на высоте 1,6 м
Видео:Закон Сохранения Энергии // Урок по Физике 7 класс - Закон Сохранения Механической ЭнергииСкачать

Переход механической энергии во внутреннюю
Внутренняя энергия — это сумма кинетической энергии хаотичного теплового движения молекул и потенциальной энергии их взаимодействия. То есть та энергия, которая запасена у тела за счет его собственных параметров.
Часто механическая энергия переходит во внутреннюю. Происходит этот процесс путем совершения механической работы над телом. Например, если сгибать и разгибать проволоку — она будет нагреваться.
Или если кинуть мяч в стену, часть энергии при ударе перейдет во внутреннюю.
Какая часть начальной кинетической энергии мяча при ударе о стену перейдет во внутреннюю, если полная механическая энергия вначале в два раза больше, чем в конце?
В самом начале у мяча есть только кинетическая энергия, то есть Емех = Ек.
В конце механическая энергия равна половине начальной, то есть Емех/2 = Ек/2
Часть энергии уходит во внутреннюю, значит Еполн = Емех/2 + Евнутр
Ответ: во внутреннюю перейдет половина начальной кинетической энергии
Видео:Закон сохранения энергии ( шары Ньютона )Скачать

Закон сохранения энергии в тепловых процессах
Чтобы закон сохранения энергии для тепловых процессов был сформулирован, было сделано два важных шага. Сначала французский математик и физик Жан Батист Фурье установил один из основных законов теплопроводности. А потом Сади Карно определил, что тепловую энергию можно превратить в механическую.
Вот что сформулировал Фурье:
При переходе теплоты от более горячего тела к более холодному температуры тел постепенно выравниваются и становятся едиными для обоих тел — наступает состояние термодинамического равновесия.
Таким образом, первым важным открытием было открытие того факта, что все протекающие без участия внешних сил тепловые процессы необратимы.
Дальше Карно установил, что тепловую энергию, которой обладает нагретое тело, непосредственно невозможно превратить в механическую энергию для производства работы. Это можно сделать, только если часть тепловой энергии тела с большей температурой передать другому телу с меньшей температурой и, следовательно, нагреть его до более высокой температуры.
Закон сохранения энергии в тепловых процессах
При теплообмене двух или нескольких тел абсолютное количество теплоты, которое отдано более нагретым телом, равно количеству теплоты, которое получено менее нагретым телом.
Математически его можно описать так:
Уравнение теплового баланса
Q отд = Q пол
Qотд — отданное системой количество теплоты [Дж]
Q пол — полученное системой количество теплоты [Дж]
Данное равенство называется уравнением теплового баланса. В реальных опытах обычно получается, что отданное более нагретым телом количество теплоты больше количества теплоты, полученного менее нагретым телом:
Это объясняется тем, что некоторое количество теплоты при теплообмене передаётся окружающему воздуху, а ещё часть — сосуду, в котором происходит теплообмен.
Задачка раз
Сколько граммов спирта нужно сжечь в спиртовке, чтобы нагреть на ней воду массой 580 г на 80 °С, если учесть, что на нагревание пошло 20% затраченной энергии.
Удельная теплота сгорания спирта 2,9·10^7Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С).
При нагревании тело получает количество теплоты
где c — удельная теплоемкость вещества
При сгорании тела выделяется энергия
где q — удельная теплота сгорания топлива
По условию задачи нам известно, что на нагревание пошло 20% затраченной энергии.
Ответ: масса сгоревшего топливаа равна 33,6 г.
Задачка два
Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре −10 °С? Потерями энергии на нагревание окружающего воздуха пренебречь. Удельная теплоемкость льда равна 2100 Дж/кг*℃, удельная теплота плавления льда равна 3,3*10^5 Дж/кг.
Для нагревания льда до температуры плавления необходимо:
Qнагрев = 2100 * 0,5 * (10-0) = 10500 Дж
Для превращения льда в воду:
Qпл = 3,3 * 10^5 * 0,5 = 165000 Дж
Q = Qнагрев + Qпл = 10500 + 165000 = 175500 Дж = 175,5 кДж
Ответ: чтобы превратить 0,5 кг льда в воду при заданных условиях необходимо 175,5 кДж тепла.
Видео:Урок 122. Закон сохранения полной механической энергииСкачать

Закон сохранения энергии для цилиндра
При решении задач по кинематике и динамики поступательного движения необходимо обратить внимание на классические законы Ньютона и границы их применения. Решая задачи, связанные с работой и энергией, повторить определения этих понятий. Необходимо понять сущность различия задач, решаемых с применением закона сохранения энергии и закона сохранения импульса. Рассматривая задачи на вращательное движение, следует обратить внимание на аналогию законов вращательного и поступательного движений, на то, что момент инерции характеризует геометрию распределения масс и не зависит от момента силы, обратить внимание на закон сохранения момента импульса.
Основные законы и формулы
| Скорость мгновенная | или |
| Ускорение: Тангенциальное | |
| Нормальное | |
| Полное | |
| Скорость угловая | |
| Ускорение угловое | |
| Уравнения равнопеременного вращательного движения | |
| Связь между линейными и угловыми величинами, характеризующими движение точки по окружности | |
| Второй закон Ньютона для поступательного движения при m = const | |
| Количество движения тела (импульс) | |
| Закон сохранения импульса для изолированной системы тел | |
| Работа переменной силы на пути S | |
| Мощность | |
| Кинетическая энергия тела | |
| Закон сохранения механической энергии | |
| Момент инерции материальной точки | |
| Момент инерции системы материальных точек | |
| полого и сплошного цилиндра радиуса R, цилиндра радиуса R, цилиндра радиуса R | |
| шара радиуса R | |
| стержня длины l | |
| Теорема Штейнера | |
| Момент силы относительно оси вращения | |
| Основные уравнения динамики вращательного движения | |
| тоже при I=const | |
| Закон сохранения момента количества движения | |
| Кинетическая энергия вращающегося тела | |
| Работа при вращательном движении | |
| Зависимость массы частицы от скорости | |
| Энергия покоя частицы | |
| Полная энергия частицы, движущейся со скоростью v , сравнимой со скоростью света | |
| Кинетическая энергия релятивистской частицы |
Читайте также: Формула по физике объем цилиндра
Примеры решения задач
Пример 1. Тело массой 1кг под действием постоянной силы, движется прямолинейно. Зависимость пути, пройденного телом, от времени задано уравнением S=2t 2 +4t+1. Определить работу силы за 10с от начала её действия и зависимость кинетической энергии от времени.
Сила, действующая на тело, по второму закону Ньютона равна:
Мгновенное ускорение определяется первой производной от скорости по времени или второй производной от пути по времени. В соответствии с этим:
Подставив (5) и (6) в уравнение (1), получим:
По этой формуле вычислим работу, совершаемую силой за 10с. С начала её действия:
Кинетическая энергия равна:
Ответ: A = 960 Дж, T = 8m (t + 1) 2
Пример 2. Сплошной цилиндр массой 0,5кг и радиусом 0,02м вращается относительно оси, совпадающей с осью цилиндра, по закону φ =12+8t-0,5t 2 . На цилиндр действует сила, касательная к поверхности. Определить эту силу и тормозящий момент.
Дано : m=0,5кг; r=0,02 м; φ =12+8t-0,5t 2
Решение: Цилиндр вращается относительно оси, совпадающей c его осью, по закону φ =12+8t-0,5t 2 . Угловое ускорение определяется как вторая производная от угла поворота по времени:
где ω — угловая скорость, равная первой производной от угла по времени: ; т.е. ω =8 — t , тогда
Момент силы относительно оси вращения: , или в скалярном виде: M=Fr· sinα , т.к. сила действует касательно к поверхности, то sinα =1 , тогда M=Fr и
Тормозящий момент можно определить из основного уравнения динамики вращательного движения:
где I — момент инерции цилиндра, относительно оси вращения, т.к. ось вращения совпадает с осью цилиндра, то момент инерции его равен:
Ответ: F = -0,005 Н, M = -10 -4 Hм
Пример 3 . Определить импульс и кинетическую энергию электрона, движущегося со скоростью 0,7с ( c — скорость света в вакууме).
Дано: m 0 =9,1· 10 -31 кг; ν =0,7с; с=3· 10 8 м/с
Решение: Импульсом частицы называется произведение массы частицы на скорость её движения:
Так как скорость электрона близка к скорости света, то необходимо учесть зависимость массы от скорости, определяемую по формуле:
где m — масса движущей частицы, m 0 — масса покоящейся частицы.
Подставляем (2) в (1) получим:
Сделаем подстановку числовых значений, входящих в формулу (3):
Кинетическая энергия T в релятивистской механике определяется как разность между полной энергией частицы E=mc 2 и её энергией покоя E 0 =m 0 c 2 , т.е. с учётом (2):
Найдём численное значение Т , подставив числовые данные в формулу (4):
Ответ: P = 2,675· 10 -22 кг· м/c, T = 3,28· 10 -14 Дж
Задачи для самостоятельного решения
1. При прямолинейном движении тела массой 1кг изменение его координаты со временем происходит по закону x=5t-10t 2 . Найти силу, действующую на тело.
2. Тело массой 3кг движется с ускорением, изменяющимся по закону a=10t-10 , v 0 =0. Определить силу, действующую на тело через 3 с после начала её действия и скорость тела в конце третьей секунды.
3. Тело движется под действием постоянной силы 15Н . Зависимость координаты от времени имеет вид: x=10-5t+2t 2 . Найти массу тела.
4. Найти зависимость скорости от времени и силу, действующую на тело массой 0,1кг в конце третьей секунды, если координата со временем изменяется по закону x=2t-t 2 +3t 3 .
5. Тело массой 2кг движется со скоростью, зависимость которой от времени выражается уравнением v=2,5t 2 +10t . Определить путь, пройденный телом за 5с и силу, действующую на тело в конце пятой секунды.
6. Сплошной шарик массой 400г и радиусом 5см вращается вокруг своей оси, проходящей через его центр. Закон вращения шара имеет вид: φ =4+2t-2t 2 . Определить вращающий момент.
7. Стержень массой 1кг и длиной 1м вращается вокруг своей оси, проходящей через один из его концов, по закону φ =2+t+t 2 . Определить момент силы, действующий на другой его конец.
8. Сплошной диск массой 0,2кг вращается вокруг своей оси, проходящей через центр его масс, под действием момента сил 0,8· 10 -2 Нм . Закон вращения имеет вид: φ =5-t+2t 2 . Определить радиус диска.
9. Полый цилиндр вращается относительно оси, совпадающей с осью цилиндра. Закон вращения имеет вид: φ =10-5t+0,5t 2 . Определить момент инерции и массу цилиндра, если его радиус 0,05м . Момент силы относительно оси вращения, действующий на цилиндр, равен 0,75Нм .
10. Шар и сплошной цилиндр имеют одинаковую массу 5кг и катятся с одинаковой скоростью 10м/с . Найти кинетические энергии этих тел.
11. Масса движущегося протона 2,25· 10 -27 кг. Найти скорость и кинетическую энергию протона.
12. Электрон прошёл ускоряющую разность потенциала 100 МВ . Во сколько раз его релятивистская масса больше массы покоя. Вычислить его полную и кинетическую энергии.
13. Определить скорость протона, если его релятивистская масса в три раза больше массы покоя. Вычислить кинетическую и полную энергии.
14. Вычислить скорость, полную и кинетическую энергии протона в тот момент, когда его масса равна массе α — частицы ( m 0α =6,44· 10 -27 кг ).
15. Найти импульс, полную и кинетическую энергии электрона, движущегося со скоростью, равной 0,9с .
16. Протон прошёл ускоряющую разность потенциалов, после чего его масса стала равна половине массы α — частицы ( m 0α =6,44· 10 -27 кг ). Определить разность потенциалов.
17. С какой скоростью движется электрон, если его кинетическая энергия равна 1,78МэВ ? Определить импульс электрона.
18. Кинетическая энергия частицы оказалась равной её энергии покоя. Какова скорость этой частицы?
19. При какой скорости масса любой частицы вещества в 5 раз больше его массы покоя?
20. Во сколько раз масса движущегося электрона, обладающего кинетической энергией 1МэВ больше его массы покоя?
21. Сплошной цилиндр массой 10кг катится без скольжения с постоянной скоростью 10м/с . Определить кинетическую энергию цилиндра и время его остановки, если на него подействует сила 50Н .
22. Стержень массой 2кг и длиной 1м может вращаться вокруг оси, проходящей через его середину перпендикулярно стержню. В конец стержня попадает пуля массой 10г , летящая перпендикулярно оси и стержню со скоростью 500м/с . Определить угловую скорость, с которой начнет вращаться стержень, если пуля застрянет в нем.
Читайте также: При микроскопии осадка мочи зернистые цилиндры имеют вид
23. Сплошной шар, скатывается по наклонной плоскости, длина которой 10м и угол наклона 30°. Определить скорость шара в конце наклонной плоскости.
24. Полый цилиндр массой 2кг катится по горизонтальной поверхности со скоростью 20м/с . Определить силу, которую необходимо приложить к цилиндру, чтобы остановить его на пути 1,6м .
25. Маховик, имеющий форму диска массой 30кг и радиусом 10см , был раскручен до частоты 300 мин -1 . Под действием силы трения диск остановился через 20с . Найти момент силы трения, считая его постоянным.
26. Автомобиль массой 5т движется равнозамедленно, при этом в течении десяти секунд его скорость уменьшается от 72км/час до 54км/час . Найти силу торможения.
27. Тело массой 1кг под действием постоянной силы движется прямолинейно. Зависимость пути, пройденного телом, от времени выражается уравнением S=t 2 +2t+2 . Определить работу силы за 5с после начала её действия.
28. В каком случае двигатель автомобиля совершит большую работу (во сколько раз): разгон с места до скорости 36км/час или увеличение скорости от 36км/час до 72км/час ? Силу сопротивления и время движения в обоих случаях считать одинаковыми.
29. Тело массой 2кг под действием постоянной силы движется и зависимость пути, пройденного телом, от времени выражается уравнением: S=t 2 +2t+2 . Найти зависимость кинетической энергии от времени и её значение в конце второй секунды.
30. Найти силу тяги, развиваемую мотором автомобиля, движущегося в гору с ускорением 1м/с 2 . Уклон горы равен 1м на каждые 25м пути. Масса автомобиля 9,8· 10 2 кг . Коэффициент трения равен 0,1.
Качественные задачи
31. Зависимость пройденного пути от времени s(t) для двух материальных точек, движущихся прямолинейно, представлена кривыми 1 и 2 (рис.1). Спрашивается, какая кривая соответствует возрастанию скорости точки, а какая — убывающей скорости?
32. Поперек реки, скорость течения которой , плывет лодка. Скорость лодки относительно воды направлена под углом к линии, перпендикулярной течению реки. Под каким углом относительно той же линии движется лодка?
33. Материальная точка движется по спирали. При этом нормальное ускорение постоянно: аn=сonst. Как изменяются линейная и угловая скорости?
34. В какую сторону вдоль оси вращения Земли направлен вектор угловой скорости при суточном её вращении?
35. Вектор угловой скорости диска направлен на восток при вращении относительно горизонтальной оси. Указать направление линейной скорости точек обода диска?
36. Пуля массой m , летящая горизонтально, попадает в подвешенный на шнуре предмет массы М . При этом возможны три случая: 1) пуля застревает в предмете, 2) пуля пробивает предмет и сохраняет только часть своей энергии, 3) пуля после удара отскакивает от предмета. В каком из этих случаев предмет поднимется на большую высоту и в каком — на наименьшую?
37. Зависит ли скорость тела у основания наклонной плоскости от угла, который она составляет с горизонтом при наличии трения или без него при скатывании этого тела без начальной скорости?
38. Два шара одинаковой массы сталкиваются (абсолютно упругий удар), испытывая нецентральный удар. Доказать, что угол между направлениями скоростей шаров после удара составляет угол 90 0 ?
39. Зависимость потенциальной энергии тел от их положения изображается параболой W p =bx 2 . По какому закону изменяются силы, действующие на эти тела?
40. У вертолетов, кроме несущего винта, на хвостовой части имеется дополнительный винт. Поясните, зачем нужен этот винт?
41. Как можно найти емкость сосуда, используя только весы и набор гирь?
42. Цилиндрический стакан до краёв наполнен жидкостью. Каким образом содержимое стакана разделить на две равные части, имея меньший сосуд произвольной формы?
43. Определите диаметр мяча линейкой.
44. Автомобиль спускается с горы с выключенным двигателем. За счет какой энергии движется автомобиль при этом?
45. Два шара разной массы, имеющие одинаковые кинетические энергии летят навстречу друг другу. В какую сторону они полетят после абсолютно неупругого столкновения? Удар лобовой.
46. Можно ли по графику зависимости пути от времени найти среднюю скорость движения м.т. по траектории?
47. Изменится ли ускорение машины, если она совершает крутой поворот с постоянной скоростью, по сравнению с ее ускорением на закруглении большего радиуса?
48. Чем отличается кинетическая энергия вращательного движения тела от кинетической энергии его поступательного движения?
49. Почему контактный провод трамвайной линии всегда идет зигзагом, а не параллельно рельсам?
50. Под каким углом разлетятся два одинаковых упругих шара после центрального удара, если один из них до удара покоился?
Контрольные вопросы
1. Дайте характеристику основных физических понятий кинематики.
2. Назовите четыре типа взаимодействий современной физики.
3. Чем характеризуется положение материальной точки в пространстве?
4. В чем различие вектора перемещения и расстояния, пройденного м.т. по траектории при ее движении?
5. Физический смысл мгновенной скорости. Как направлен вектор мгновенной скорости?
6. Физический смысл мгновенного ускорения. Как направлен вектор мгновенного ускорения?
7. Физический смысл нормального, тангенциального, полного ускорения. Как направлено каждое из них?
8. В чем заключается физический смысл угловой скорости?
9. Как связаны линейная и угловая скорости в векторном виде?
11. Что такое импульс м.т. (тела)?
12. Сформулируйте закон всемирного тяготения и его границы применения.
13. Преобразования Галилея и принцип относительности.
14. Принцип независимости действия сил.
16. Что такое кинетическая энергия и как она связана с работой?
17. Сформулируйте закон сохранения механической энергии.
18. Cформулируйте теорему Штейнера-Гюйгенса.
19. Сформулируйте закон сохранения вектора момента импульса.
20. Запишите формулу работы тел при вращательном движении.
© ФГОУ ВПО Красноярский государственный аграрный университет, 2015
📽️ Видео
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ в механике класс физика ПерышкинСкачать

Закон сохранения энергии. 9 класс. Решение задачСкачать

Закон сохранения и превращения энергии. 9 класс.Скачать

Урок 126. Задачи на закон сохранения энергии (ч.1)Скачать

Закон сохранения энергии в механике | Физика 10 класс #21 | ИнфоурокСкачать

Вывод закона сохранения механической энергии | Физика 9 класс #22 | ИнфоурокСкачать

Закон сохранения импульсаСкачать

Как нарушить закон сохранения энергии?Скачать

Закон сохранения энергии | Образовательный семинар доктора БожьеваСкачать

7 класс, 15 урок, Энергия. Закон сохранения энергииСкачать

Студенты российского вуза разработали вечный двигатель #вечныйдвигатель #изобретенияСкачать

Урок 125. Работа, мощность и кинетическая энергия при вращательном движенииСкачать

Закон сохранения и превращения механической энергии. 7 класс.Скачать

Закон сохранения превращения энергии в тепловых процессах. 8 класс.Скачать