Зависимость числа струхаля от числа рейнольдса для круглого цилиндра

Видео:ОВР и Метод Электронного Баланса — Быстрая Подготовка к ЕГЭ по ХимииСкачать

Зависимость числа струхаля от числа рейнольдса для круглого цилиндра

СРЫВНЫЕ ТЕЧЕНИЯ ЖИДКОСТНОЙ И ГАЗОВОЙ ФАЗ

Евгений Николаевич Беляев, к.т.н., МАИ

Валерий Васильевич Черваков, д.т.н., МАИ

Создание новой ракетно-космической техники всегда сопряжено с риском принятия неверных решений, приводящих к тяжелым аварийным ситуациям. Без этого не обходится ни одна из отраслей промышленности, будь то авиационная, атомная или судостроительная промышленность. Путь в космическое пространство вымощен обломками ракетно-космической техники, разрушением испытательных стендов и стартовых комплексов, омрачен гибелью отважных космонавтов и астронавтов. Одной из причин тяжелых аварийных ситуаций, совершенно непредсказуемых, являлось возникновение колебаний элементов конструкции или давлений компонентов топлива в жидкостном ракетном двигателе (ЖРД) приводившие к его разрушению. Причиной возникновения таких колебаний были разные, в их числе, срывы вихрей при течении жидкостной или газовой фаз. В технике, и в первую очередь, в авиационной, с этой проблемой столкнулись 1930-х гг., когда по миру прокатилась волна странных аварий при испытаниях скоростных самолетов. Летчики испытатели, которым посчастливилось остаться в живых, и очевидцы наблюдали почти одну и ту же картину: самолет летел нормально, как вдруг какая-то неведомая сила, будто взрывом, разрушала машину. Этому всегда предшествовало интенсивное увеличение вибраций самолета с нарастающей амплитудой. Это таинственное и грозное явление назвали «флаттер» (от английского flutter — дрожание). Ученые, и в частности М.В. Келдыш, довольно быстро разобрались, что флаттер порождается взаимодействием в конструкции упругих, инерционных и аэродинамических сил.

Плохое обтекание крыла самолета может привести к неустойчивости — срывному флаттеру. На современных самолётах он может произойти в условиях обледенения, когда поверхность крыла, в частности его передняя кромка, покрывается ледяной коркой произвольной формы. Характер обтекания резко ухудшается, и за крылом может формироваться периодическая система вихрей — “дорожка Кармана”, которая вызывает колебания крыла. Фон Карманом экспериментально установлено [1], что при обтекании цилиндрических тел, или плоских пластин, установленных под некоторым углом к набегающему потоку, происходят поперечные колебания зоны отрыва течения (срыв вихрей). При этом зона пониженного давления оказывается то с одной, то с другой стороны от направления движения, в результате на тело действует не только продольная сила лобового сопротивления, но и переменная поперечная сила.

Явление отрыва связано с большими градиентами давления и скорости течения в пограничном слое. Отрыв потока обычно возникает в точках максимальной скорости и, следовательно, минимального давления, после чего это низкое давление доминирует во всей зоне отрыва ниже по течению [2].

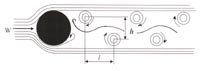
Карман теоретически показал, что картина расположения вихрей (вихревых следов) стабильна, если отношение поперечного расстояния между ними h к продольному расстоянию l (рис. 1) составляет h/l = 0,28.

Вихревые следы встречаются повсеместно. Их можно создать в лабораторных условиях, можно наблюдать в природе.

Говоря о срывном флаттере, следует отметить, что чаще всего он возникает тогда, когда частота схода вихрей приближается к одной из собственных частот конструкции. В этом случае возникают резонансные колебания, которые могут приводить к разрушению конструкции.

Срывной флаттер наблюдался неоднократно у целого ряда технических сооружений: многих подвесных мостов, заводских труб, винтов вертолетов, перископов подводных лодок, лопаток компрессоров, турбин в турбореактивных двигателях, на днищах ракет, проводах высоковольтных линий и т.п. Он приводил к различным катастрофам, среди наиболее известных, это разрушение Такомского моста [3]. Случилось это в ноябре 1940 года в США. Такомский мост простоял всего несколько месяцев и был полностью разрушен 7 ноября (рис. 2). Причиной разрушения стали многочисленные дорожки Кармана, которые отрывались от силовых тросов, напоминающих огромные вертикальные струны. При скорости ветра 19 м/с, установились одноузловые изгибно-крутильные колебания полотна моста с такой амплитудой, что угол наклона проезжей части к горизонту достигал 45°. После часа таких колебаний часть проезжего полотна отломилась и рухнула в воду.

Читайте также: Ford 1863548 цилиндр сцепления главный

Частота срыва вихрей определяется числом Струхаля

где W — скорость набегающего потока,
f — частота вихреобразования,
l — характерный размер (например, диаметр цилиндра или ширина пластины) [1].

Число Струхаля — безразмерная величина, один из критериев подобия нестационарных течений жидкостей и газов, характеризующий постоянство протекания процессов во времени.

Экспериментально установлено, что число Струхаля является безразмерной частотой генерации вихрей и связано с числом Рейнольдса для потока, порождающего след. Для ламинарного режима (режим I), переходного режима (режим II) и третьего режима (режим III), в котором поток не реагирует с одной единственной частотой, но число Струхаля соответствует частоте с максимальной энергией соотношением Sh = 0,2175 — 5,1064/Re для ламинарного режима течения (до Re = 200) и Sh = 0,212 — 2,7/Re для больших значений Re равных 400 и выше. Последняя аппроксимация содержит предельное (0,212) число Струхаля при больших значения числа Re [4].

В работе [4] приведены экспериментальные данные (рис. 3), по которым получены выше приведенные соотношения между числами Струхаля и Рейнольдса.

Проблеме срыва вихрей и генерации звука посвящено очень большое количество работ начиная с конца ХIX века по сегодняшний день. На рис. 4 приведены экспериментальные данные, полученные разными авторами и в разное время [5], зависимости числа Струхаля от числа Рейнольдса.

На графике хорошо видно, что в диапазоне 4·102

Видео:Урок 138. Число Рейнольдса. Критерий Рейнольдса.Скачать

Число Струхаля — Strouhal number

В размерном анализе число Струхаля ( St или иногда Sr, чтобы избежать конфликта с числом Стентона ) является безразмерным числом, описывающим механизмы колебательного потока. Параметр назван в честь Винченка Струхаля , чешского физика, который в 1878 году экспериментировал с проводами, которые испускали вихри и пели на ветру. Число Струхаля является неотъемлемой частью основ механики жидкости .

Число Струхаля часто выражается как

где f — частота образования вихрей , L — характерная длина (например, гидравлический диаметр или толщина профиля ), U — скорость потока . В некоторых случаях, например, в полете с опусканием вниз, эта характерная длина является амплитудой колебаний. Этот выбор характеристической длины может использоваться, чтобы представить различие между числом Струхаля и приведенной частотой:

где k — приведенная частота , а A — амплитуда качающихся колебаний.

Для больших чисел Струхаля (порядка 1) вязкость преобладает над потоком жидкости, что приводит к коллективному колебательному движению жидкой «пробки». Для низких чисел Струхаля (порядка 10 -4 и ниже) высокоскоростная, квазистационарная часть движения доминирует над колебанием. Колебания при промежуточных числах Струхаля характеризуются нарастанием и быстрым последующим отрывом вихрей.

Для сфер с равномерным потоком в диапазоне чисел Рейнольдса 8 × 10 2 5 сосуществуют два значения числа Струхаля. Более низкая частота объясняется крупномасштабной неустойчивостью следа, не зависит от числа Рейнольдса Re и приблизительно равна 0,2. Более высокочастотное число Струхаля вызвано мелкомасштабной нестабильностью от отделения сдвигового слоя.

Видео:Лайфхаки ЕГЭ по математике: решения и ответы | Задание 8: цилиндр | Быстрая подготовка к ЕГЭСкачать

Приложения

Метрология

В метрологии , особенно в турбинных счетчиках с осевым потоком , число Струхаля используется в сочетании с числом Рошко для установления корреляции между расходом и частотой. Преимущество этого метода перед методом зависимости частоты / вязкости от К-фактора заключается в том, что он учитывает влияние температуры на измеритель.

f = частота измерителя, U = расход, C = линейный коэффициент расширения материала корпуса счетчика.

Это соотношение оставляет Струхаля безразмерным, хотя для C 3 часто используется безразмерное приближение , приводящее к единицам импульсов / объема (то же, что и K-фактор).

Передвижение животных

У плавающих или летающих животных число Струхаля определяется как

f = частота колебаний (биение хвостом, взмахи крыльев и т. д.), U = расход, A = размах колебаний.

При полете или плавании животных эффективность движения высока в узком диапазоне констант Струхаля, обычно достигая пика в диапазоне 0,2 гребков , A — амплитуда, поэтому числитель fA равен половине вертикальной скорости законцовки крыла, а знаменатель V — горизонтальная скорость. Таким образом, график законцовки крыла образует приблизительную синусоиду с удлинением (максимальным наклоном), вдвое превышающим постоянную Струхаля.

Читайте также: Главный тормозной цилиндр передний мото

Видео:Задание 10 ЕГЭ по математике #4Скачать

Число Струхаля

Число Струхаля ( [1] [2] [3] , также [4] или ) — безразмерная величина, один из критериев подобия нестационарных (часто колебательных) течений жидкостей и газов. Для колебательных процессов число Струхаля обычно определяется соотношением

где — характерная частота процесса (например, частота образования вихрей), — характерный линейный размер течения (например, гидравлический диаметр), — характерная скорость потока. Для непериодических процессов часто используется определение [1] [4]

где — характерное время процесса. Иногда числом Струхаля называется обратная величина [5] [6] (число гомохронности [7] [8] )

Видео:Нормальное Распределение за 6 МинутСкачать

Варианты названия и произношение

Наряду с названием число Струхаля [3] [1] в литературе встречается вариант число Струхала [5] . Ударение в слове Струхаль (Струхал) не установилось: в речи встречается как ударение на первый слог, соответствующее языку-источнику [9] , так и на второй.

Видео:✓ RSA на пальцах: Криптография или зачем нужна математика | Ботай со мной #033 | Борис ТрушинСкачать

Историческая справка

Число Струхаля было введено Рэлеем 1894 г. [10] при теоретическом описании результатов опытов Строугала (Струхаля) по изучению генерации звука при обдувании цилиндрических тел потоком воздуха [11] . Название число Струхаля было, по-видимому, введено Рэлеем в 1915 г. [12] .

Видео:ЭТОТ метод поможет на уроках ХИМИИ / Химия 9 классСкачать

Механический смысл

Число Струхаля характеризует [13] порядок отношения локальной производной и конвективной производной , входящих в полную производную в уравнении движения. Если число Струхаля мало, , то слагаемым, содержащим производную по времени, можно пренебречь, приближенно рассматривая течение как стационарное или квазистационарное. В противоположном случае существенно нестационарного процесса () можно пренебречь конвективной производной, что в ряде случаев существенно упрощает теоретический анализ (например, в случае движения вязкой жидкости после такого упрощения нелинейные уравнения Навье — Стокса становятся линейными).

Видео:Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать

Применение для описания автоколебаний тела в потоке жидкости или газа

При описании автоколебаний тел в потоках жидкости и газа (звучание эоловой арфы, флаттер, галопирование) число Струхаля, являющееся, фактически, безразмерной частотой колебания тела, зависит от числа Рейнольдса и других параметров. В случае поперечного обтекания цилиндра, важном с практической точки зрения (действие ветра на провода, башни, ракеты на стартовых позициях), число Струхаля зависит только от числа Рейнольдса, причём в диапазоне (см. рис.) действует приближенный эмпирический закон постоянства числа Струхаля: .

Видео:4 класс, 23 урок, Нахождение части числаСкачать

Примечания

1. ↑ 123Лойцянский Л. Г. Механика жидкости и газа. — М .: ГИТТЛ, 1957. — С. 472. — 784 с.
2. ↑Седов Л. И. Методы подобия и размерности в механике. — М .: Наука, 1981. — С. 75. — 448 с.
3. ↑ 12Слёзкин Н. А. Динамика вязкой несжимаемой жидкости. — М .: ГИТТЛ, 1955. — С. 107. — 520 с.
4. ↑ 12Вольмир А. С. Оболочки в потоке жидкости и газа. Задачи гидроупругости. — М .: Наука, 1979. — С. 123. — 320 с.
5. ↑ 12Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. — М .: Наука, 1986. — Т. 6. Гидродинамика. — С. 89. — 736 с.
6. ↑Микишев Г. Н. Экспериментальные методы в динамике космических аппаратов. — М .: Машиностроение, 1978. — С. 134. — 248 с.
7. ↑Кутателадзе С. С. Анализ подобия в теплофизике. — Новосибирск: Наука, 1982. — С. 259. — 280 с.
8. ↑Михеев М. А., Михеева И. М. Основы теплопередачи. — М .: Энергия, 1977. — С. 63. — 344 с.
9. ↑ В чешском языке ударение падает на первый слог. Ср. ударение в заимствованных именах собственных Гашеек, Чапек, Шкода.
10. ↑Стретт Дж. В. (лорд Рэлей)Теория звука. — М .: ГИТТЛ, 1955. — Т. 2. — С. 400. — 476 с.
11. ↑Strouhal Ueber eine besondere Art der Tonerregung // Ann. Der Physik u. der Chemie (Wiedemann’s Ann.). — 1878. — Т. 5. — С. 216–251. (Реферат на французском языке)
12. ↑RayleighÆolian tones // Philosophical Magazine. — 1915. — Т. 29. — С. 433-444.
13. ↑Баранов В. Б. Гидроаэромеханика и газовая динамика. Часть I. — М .: Издательство МГУ, 1987. — С. 80–81. — 184 с.
14. ↑ Данные из книги: Современное состояние гидроаэродинамики вязкой жидкости / Под ред. С. Гольдштейна. — М .: ИЛ, 1948. — Т. 2. — С. 96, 98, 248. — 408 с. См. также экспериментальные данные в курсе по вычислительным методам в гидромеханике (фр.) .

Читайте также: После замены грм нет компрессии в одном цилиндре

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Число Струхаля» в других словарях:

число Струхаля — Strouhalo skaičius statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. Strouhal number vok. Strouhalsche Zahl, f; Strouhal Zahl, f rus. число Струхаля, n pranc.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

число Струхаля — Strouhalo skaičius statusas T sritis fizika atitikmenys: angl. Strouhal number vok. Strouhalsche Zahl, f; Strouhal Zahl, f rus. число Струхаля, n pranc. nombre de Strouhal, m … Fizikos terminų žodynas

число Струхаля — Безразмерное число, равное отношению произведения частоты и линейного размера к величине скорости … Политехнический терминологический толковый словарь

Число Уомерсли — (Wo или α) критерий подобия в гидродинамике, определяющий соотношение между темпом пульсации потока жидкости и её вязкостью. Оно определяется следующим образом: , где характеристическая длина; период пульсаций; угловая… … Википедия

Число Струхала — Зависимость числа Струхаля от числа Рейнольдса Число Струхаля безразмерная величина, один из критериев подобия нестационарных течений жидкостей и газов, характеризующий постоянство протекания процессов во времени. Одна из формул, описывающих… … Википедия

Число струхала — Зависимость числа Струхаля от числа Рейнольдса Число Струхаля безразмерная величина, один из критериев подобия нестационарных течений жидкостей и газов, характеризующий постоянство протекания процессов во времени. Одна из формул, описывающих… … Википедия

СТРУХАЛЯ ЧИСЛО — (по имени чеш. учёного В. Струхаля (Строугаль; V. Strouhal)), подобия критерий нестационарных движений жидкостей или газов. Характеризует одинаковость протекания процессов во времени: Sh=l/vt=wl/v, где l, v характерные линейный размер и скорость… … Физическая энциклопедия

Число Ричардсона — ( ) критерий подобия в гидродинамике, равный отношению потенциальной энергии тела, погружённого в жидкость к его кинетической энергии. Под «телом» здесь обычно понимается рассматриваемая жидкость или газ. В общем случае число Ричардсона… … Википедия

Число Дамкёлера — ( ) критерий подобия в химии, определяющий отношение скорости течения химической реакции к скорости других процессов, происходящих в системе. В общем случае его можно выразить как отношение характерного времени физического процесса к характерному … Википедия

Число Рейнольдса — Число, или, правильнее, критерий Рейнольдса ( ), безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье Стокса[1]. Число Рейнольдса также считается критерием подобия течения вязкой… … Википедия

🎦 Видео

Простой ребус для простого человека ★ Сможет решить каждыйСкачать

Как выучить Химию с нуля за 10 минут? Принцип Ле-ШательеСкачать

Что такое математическая последовательность? | Математика | TutorOnlineСкачать

Формула для приближенных вычисленийСкачать

Пропорциональные отрезки круга. 9 класс.Скачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Вас обманывают насчет ЗОЛОТОГО СЕЧЕНИЯ!Скачать

Супер ЖЕСТЬ для продвинутых: sqrt(2+sqrt(2-sqrt(2+x)))=xСкачать

Распределение Гаусса.Скачать

Уравнение Нернста. Задачи на расчет потенциалов. Продукты в ОВР. Ч.5-2.Скачать

ВСЕ про теорию Вероятностей | ЕГЭ профиль номера 4 и 5 | Ильич ЕГЭ Профильная математикаСкачать