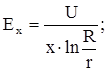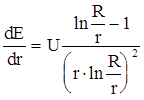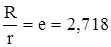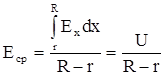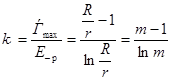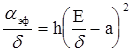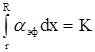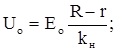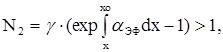Зависимость напряжения от расстояния до оси цилиндров (3 видео)

Видео:Студенты российского вуза разработали вечный двигатель #вечныйдвигатель #изобретенияСкачать

Начальное и пробивное напряжение в цилиндрической системе электродов

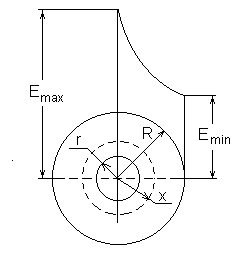
Цилиндрическая система электродов представляет собой коаксиальную (соосную) систему цилиндров (см, рис. 2).

Рис. 2. Цилиндрическая система электродов

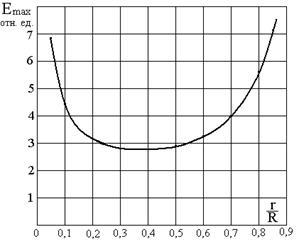
Напряженность поля в промежутке между цилиндрами изменяется по уравнению, графическая зависимость которого приведена на рис. 2 :

Напряженность поля у внутреннего проводника будет максимальной, а у внешнего — минимальной:

;

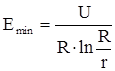
Если напряжение U и R заданы, то можно определить значение r, при котором максимальная напряженность в промежутке будет минимальна, т. е. пробивное значение напряжения максимально (условие наибольшей электрической прочности цилиндрической системы). С этой целью дифференцируем Еmax по r:

Для получения минимума приравняем полученное выражение нулю:

, откуда

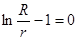
Таким образом, у цилиндрической системы с максимальной электрической прочностью отношение диаметров внутреннего и внешнего проводников должно равняться 2,72.

Цилиндрическая система характеризуется коэффициентом неоднородности , т. е. отношением максимальной напряженности к средней, равной:

Промежутки, в которых > 4, называются коронирующими или промежутками с резконеоднородным полем. Соотношение радиусов цилиндров при этом R/r > 10,5.

Рассмотрим условия возникновения самостоятельного разряда в цилиндрической системе электродов. Данная задача актуальна, поскольку в энергетике большое число конструкций имеет именно такую систему.

На предыдущем занятии рассмотрена зависимость эффективного коэффициента ударной ионизации от напряженности поля и конструктивных параметров при атмосферном давлении, которая приведена к эмпирической зависимости:

где h и а — постоянные и для воздуха равны: h = 0,2 см/ква , а = 24 кВ/см.

Для системы электродов условие самостоятельности разряда есть интеграл по промежутку, который равен постоянной. Для цилиндрической системы:

Данные уравнения имеют решения, которые приведены к эмпирическим зависимостям, удобным для практических расчетов.

Амплитудное значение начального напряжения, кВ, в цилиндрической системе электродов для воздуха при отрицательной полярности внутреннего цилиндра (в этом случае пробивное напряжение максимально), а также переменном напряжении определяется по следующим формулам:

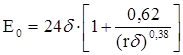
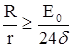
а) при (1)

б) где при (2)

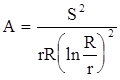
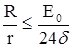
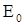
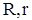
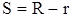
Здесь — начальная напряженность, кВ/см, равная напряженности на поверхности внутреннего цилиндра при начальном напряжении; и — размеры цилиндрической системы электродов.

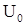
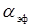
Наличие двух формул для расчета начального напряжения объясняется тем, что эффективная ионизация ( > 0) может иметь место либо только в части промежутка (случай “а”, резконеоднородное поле ), либо по всей длине промежутка (случай “б”, однородное поле). а следовательно пределы интегрирования в уравнении самостоятельного разряда:

Читайте также: Как собрать главный тормозной цилиндр ваз 2106

из которого получены выражения (1) и (2), будут различными.

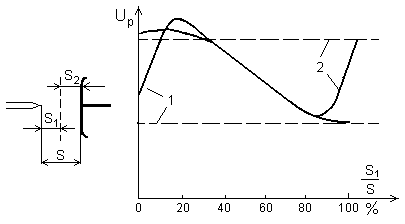
Если радиус наружного цилиндра R сохранять постоянным, а радиус внутреннего цилиндра увеличивать, то начальное напряжение вначале будет возрастать, а затем снижаться до нуля (кривая 1, рис. 3).

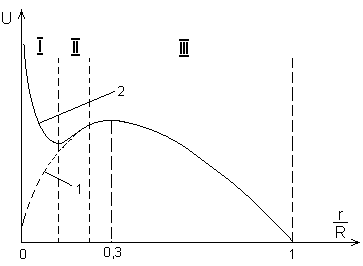
Рис. 3. Зависимости начального (1) и пробивного (2) напряжений от отношения радиусов внутреннего и наружного коаксиальных цилиндрических электродов.

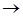
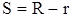
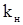
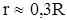
Это объясняется тем, что при увеличении r происходит как уменьшение коэффициента неоднородности ( 1), так и уменьшение длины промежутка , , причем при малых r основное влияние оказывает (начальное напряжение вследствие этого увеличивается), а начиная с преобладающее влияние оказывает уменьшение длины промежутка (вследствие этого растет напряженность и уменьшается).

Зависимость пробивного напряжения промежутка от величины радиуса внутреннего цилиндра более сложная (кривая 2, рис. 3). Эта зависимость может быть разделена на три области:

область III — поле близкое к однородному и поэтому пробивное напряжение совпадает с начальным;

область II — поле резконеоднородное и вследствие этого пробивное напряжение несколько превышает начальное. Корона здесь имеет стримерный характер сразу после ее возникновения, следовательно одно из условий пробоя промежутка — образование стримера — здесь уже выполнено. Вследствие этого величина пробивного напряжения близка к начальному напряжению. снижение пробивного напряжения при уменьшении r связано с уменьшением начального напряжения;

область I — так же, как и в области II, поле резконеоднородное, но корона при возникновении имеет лавинный характер. Для пробоя промежутка необходимо появление стримера, но, как показывают эксперименты. с уменьшением радиуса внутреннего цилиндра напряжение появления стримера (переход короны из лавинной формы в стримерную) возрастает, что приводит к увеличению пробивного напряжения промежутка.

Влияние диэлектрического барьера на пробивные напряжения резконеоднородного промежутка

Барьером называется диэлектрик (например, бумага), который помещается между электродами перпендикулярно центральной силовой линии электрического поля (для промежутка стержень — плоскость, который и будет рассматриваться ниже, центральная силовая линия совпадает с осью симметрии электрического поля промежутка). Изменение пробивного напряжения промежутка при наличии барьера вызвано изменением картины поля в промежутке в следствие осаждения ионов на поверхность барьера.

Если в качестве барьера использовать изоляционный материал, пробивное напряжение которого соизмеримо с пробивным напряжением промежутка, то за счет электрической прочности барьера суммарная электрическая прочность промежутка повышается. Пробивное напряжение промежутка при наличии барьера зависит от полярности электрода и расположения барьера в промежутке.

Читайте также: Гильза цилиндра фиат дукато

Рис. 3. Зависимость пробивного напряжения от положения барьера для промежутка стержень — плоскость с барьером.

1 — положительный стержень; 2 — отрицательный стержень. S1 — расстояние от стержня до барьера.

напряжение электрод разряд диэлектрический

Соответствующие зависимости для промежутка стержень — плоскость приведены на рис. 3. Пунктиром показаны пробивные напряжения при отсутствии барьера.

Если барьер расположен у стержня и касается его, от, т. к. барьер имеет хотя и малую, но конечную толщину, ионизация в области наибольшей напряженности поля, занятой барьером, будет невозможна. Следовательно, для возникновения коронного разряда и последующего пробоя промежутка требуется увеличить напряжение. Увеличение пробивного напряжения зависит от толщины карьера.

Если барьер установлен на некотором расстоянии от стержня, то он не повлияет на напряжение возникновения коронного разряда. Коронный разряд, возникающий у стержня, приводит к появлению между стержнем и барьером объемного заряда (электронов и положительных ионов), причем заряды, имеющие знак, противоположный знаку стержня, движутся к нему и нейтрализуются на нем, а заряды того же знака движутся к барьеру и осаждаются на его поверхности. Заряды, осевшие на барьере, снижают напряженность электрического поля у стержня, и если напряжение на промежутке не увеличивается, то коронный разряд прекращается. При увеличении напряжения величина заряда на барьере будет возрастать, а следовательно, будет увеличиваться напряженность электрического поля между барьером и плоскостью, что приведет к пробою между ними, а значит и к пробою всего промежутка.

Наибольшая напряженность электрического поля и наибольшее количество зарядов в лавинах будут на центральной силовой линии. Вследствие этого наибольшая плотность осевшего на поверхность барьера заряда будет в точке пересечения центральной силовой линии поля с барьером. Поле , создаваемое осевшим на барьер зарядом, в этом случае можно в первом приближении приравнять эквивалентным полю шара с радиусом S1 , равным расстоянию от стержня до барьера (рис. 3).

Таким образом, пробивное напряжение промежутка стержень — плоскость длиной S с барьером может быть определено как сумма двух напряжений: напряжения между стержнем и барьером и пробивного напряжения промежутка эквивалентный шар радиусом S1 — плоскость при длине промежутка S2 , равной расстоянию между барьером и плоскостью. напряжение между стержнем и барьером практически не отличается от начального напряжения этого промежутка, т. к. заряд, осевший на поверхность барьера, снижает напряженность у стержня до начальной. Следовательно, пробивное напряжение промежутка стержень — плоскость с барьером определяется главным образом электрической прочностью промежутка барьер — плоскость (эквивалентный шар — плоскость).

Читайте также: Цилиндры с полным штоком

Поле промежутка шар — плоскость более однородно, поэтому его пробивное напряжение будет выше, чем у исходного промежутка стержень — плоскость. С удалением барьера от стержня радиус шара эквивалентного промежутка шар — плоскость возрастает, что приводит к увеличению однородности поля и возрастанию пробивного напряжения. Возрастание пробивного напряжения будет происходить примерно до тех пор, пока поле эквивалентного промежутка шар — плоскость не станет слабонеоднородным, что соответствует S2 / S1

Видео:НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ суперпозиция полейСкачать

Найти зависимость напряженности электрического поля от расстояния, отсчитываемого от оси цилиндров

2)На двух коаксиальных бесконечных цилиндрах радиусами R = R 1 и R2 2R = равномерно распределены заряды с поверхностными плотностями соответственно 20 нКл/м2 и –80 нКл/м2. Найти зависимость напряженности электрического поля от расстояния, отсчитываемого от оси цилиндров, превышающего радиус второго цилиндра.

помогите пожалуйста с решениями

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Найти зависимость напряжённости электрического поля от расстояния
Кольцо из проволоки радиусом 10 см имеет отрицательный заряд -5,0 нКл. Найти зависимость.

Найти зависимость от времени напряженности электрического поля в конденсаторе
Плоский воздушный конденсатор с площадью пластин 50 см² включен последовательно в цепь переменного.

Найти напряженности электрического поля в точках, удаленных от центра шара на расстояния 2 см и 10 см
Стеклянный шар равномерно заряжен по всему объему. Радиус шара 5 см, заряд – 2 мкКл. Шар помещен в.

Определить зависимость напряженности электрического поля
Определите зависимость напряженности электрического поля, что создается равномерно заряженным слоем.

Найти зависимость от расстояния до нити объемной плотности энергии электрического поля нити
Помогите с задачкой, пожалуйста. Бесконечно длинная нить заряжена с линейной плотностью заряда.

Найти зависимость напряженности и потенциала от расстояния до центра шара (внутри и вне)
2.Диэлектрический шар радиусом R и проницаемостью равной 1 равномерно заряжен по объему зарядом Q.

Найти величину напряженности электрического поля
Тонкое кольцо радиуса R несет равномерно распределенный заряд q. Найти величину напряженности.