Значение цилиндра в нашей жизни (2 видео)

Цилиндры вокруг нас. «Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг — геометрия» Ле Корбюзье. И правда, если мы посмотрим вокруг, мы увидим, что нас окружают одни лишь геометрические тела, в частности цилиндры. Цилиндр может быть стаканом или гвоздем или быть частью архитектурной постройки или сложного механизма.

Слайд 27 из презентации «Понятие цилиндра». Размер архива с презентацией 1056 КБ.

Содержание

Геометрия 11 класс
Безумный шляпник, и ещё об истории цилиндра
Ровно 220 лет назад, 15 января 1797 года, шляпный мастер Джеймс Хетерингтон впервые вышел из своего дома Лондоне с цилиндром на голове.
Мастерство и слабоумие
Цилиндр в архитектуре
Содержимое разработки
Презентация по геометрии на тему «Цилиндр и его элементы»(11 класс)
🎦 Видео

Видео:Подбор цилиндра. Почему цилиндр подбирается ТОЛЬКО в минусе.Скачать

Геометрия 11 класс

«Задачи по стереометрии» — Длина окружности. Объм шара и его частей. Диаметр свинцового шара. Найдите объем пирамиды. Найдите площадь поверхности многогранника. Найдите угол многогранника. Найдите квадрат расстояния между вершинами. Найдите объем V части цилиндра. Задачи. Круговой сектор. Найдите ординату точки A. Найдите площадь трапеции.

««Задачи по геометрии» 11 класс» — Ответим устно. Проблема. Около правильной шестиугольной призмы описана сфера радиуса 5 см. Призма. Многогранники, описанные около шара. Основанием треугольной пирамиды является прямоугольный треугольник. В правильную четырехугольную усеченную пирамиду вписан шар. Найдите радиус вписанной в правильную шестиугольную призму сферы. Измерения прямоугольного параллелепипеда. Технология проекта. Около треугольной призмы описана сфера, центр которой лежит вне призмы.

«Философ Пифагор» — Истина. Математика. Жизнь и научные открытия Пифагора. Слово «философ». Пифагор встречался с персидскими магами. Мнесарх. Основоположник современной математики. Пифагор. Девиз. Бессмертная идея. Мысль. Знание основ музыки. Египетские храмы. Направление полёта.

«Площадь сферы» — Радиус описанного шара равен половине диагонали куба: Диаметр шара (d=2R). Vш. сектора= 2/3ПR2h. Решение. Шаровой сектор состоит из шарового сегмента. описан шар. От данной точки (C). Тогда объем шара. раза больше площади поверхности большого круга. По построению радиусы шара и основания цилиндра равны. Объем шара радиуса. Равен. Радиус большого круга является радиусом шара. Высота сегмента (h). Сегмента = Пh2(R- 1/3h).

««Прямоугольный параллелепипед» геометрия» — Объем куба равен 64. Найдите объём многогранника. Найдите площадь поверхности многогранника. Формулы полной поверхности и объёма прямоугольного параллелепипеда. Все двугранные углы прямые. Прямоугольный параллелепипед. Прямоугольный параллелепипед в задачах В9 и В11 ЕГЭ. Найдите объём. Найдите квадрат расстояния между вершинами. Найдите угол CAD.

««Векторы» 11 класс» — История возникновения понятия вектор. Равенства. На рисунках вектор изображается отрезком со стрелкой. Вектор называется свободным, если его значение не меняется. Абсолютная величина вектора. Коллинеарные векторы. Сумма двух векторов. Примером скользящего вектора может служить сила. Пример. Векторы. Правило параллелограмма. Правило треугольника. Длиной или модулем ненулевого вектора АВ называется длина отрезка АВ.

Всего в теме «Геометрия 11 класс» 45 презентаций

Видео:ОБЪЯСНЕНИЕ МИРА, ОТКУДА ПРИШЕЛ ЦИЛИНДР ( The Eternal Cylinder )Скачать

Безумный шляпник, и ещё об истории цилиндра

Видео:Академия Shamir. УТОЧНЕНИЕ ЦИЛИНДРАСкачать

Ровно 220 лет назад, 15 января 1797 года, шляпный мастер Джеймс Хетерингтон впервые вышел из своего дома Лондоне с цилиндром на голове.

Появление мужчины шокировало окружающих: барышни теряли сознание, дети кричали, собаки разрывались от лая. Тот день для первого цилиндроносца закончился не слишком удачно: одного из обескураженных очевидцев его шляпного дебюта сбили с ног и он сломал руку. Виновника доставили в полицию и присудили уплатить штраф 500 фунтов стерлингов.

Несмотря на провальный дебют, цилиндр последующие 100 лет оставался наиболее популярным предметом шляпного гардероба у мужчин.

Известный шляпный модельер Ирина Белопухова рассказала Лайфу об истории создания цилиндра и его значении.

— Цилиндр — один из самых интересных и важных головных уборов в истории. Он давал мужчине то, что ему всегда нужно, — высокий рост. Соответственно, и значительность в образе. Вот, например, Пушкин очень любил и всегда ходил в высоком цилиндре (рост Пушкина составлял примерно 165 см. — Прим. Лайфа). Эта шляпа вытягивает фигуру и придаёт ей стать, вот в чём её секрет, — рассказала Белопухова.

Читайте также: Как проверить передний тормозной цилиндр ваз 2106

Видео:4.3. Сила цилиндраСкачать

Мастерство и слабоумие

Не только Джеймс Хетерингтон пострадал от цилиндра. Недорогие модели этих шляп в XIX веке часто изготавливали из фетра. А для того, чтобы материал держал форму, его обрабатывали специальным раствором на основе ртути и других ядовитых веществ. При длительном вдыхании этих паров поражалась центральная нервная система — и человек потихоньку сходил с ума. Это не сразу заметили, но когда обратили внимание, что поведение многих шляпников становится неадекватным, приняли меры. Оказывается, безумный шляпник в «Алисе в стране чудес» взялся у Кэррола не просто так.

Самым популярным цветом у цилиндров был и остаётся чёрный, но носили эти шляпы и других цветов — например, летом были приняты серые головные уборы. До сих пор на протокольных скачках в Аскоте, Баден-Бадене и других мужчины появляются обязательно в серых цилиндрах.

Когда английская королева Елизавета II посещала в 1994 году Москву, она привезла с собой собственный автомобиль Rolls Royce с очень высоким верхом — она везде его возит с собой, — и именно в нём супруг мог ездить в цилиндре.

Поскольку цилиндры высокие и занимали много места, придумали его складную разновидность — внутрь тульи помещали хитрую конструкцию, которая помогала складывать шляпу буквально в плоский диск. Для того чтобы его раскрыть, резко им взмахивали — и конструкция производила странный звук типа «кляк». По-русски эта «шапка, издающая кляк» звучит как «шапокляк».

В XX веке цилиндр постепенно перешёл в женский костюм. Марлен Дитрих была в цилиндре в своей знаменитой роли в «Голубом ангеле», и именно оттуда свой образ почерпнула Любовь Орлова для «Весёлых ребят». Вернее, этот образ в фильм привнёс режиссёр Григорий Александров, у которого до брака с Орловой был роман с Дитрих.

Но первыми женщинами, надевшими эту мужскую шляпу, были не они. Французская писательница Жорж Санд, ещё в XIX веке эпатировавшая свет появлением в мужском костюме, очень любила этот вид головного убора. Отечественная амазонка Серебряного века Зинаида Гиппиус тоже не брезговала цилиндром.

Шанс вернуться в повседневную жизнь людей у цилиндра есть едва ли, утверждает Ирина Белопухова. Впрочем, мода иногда принимает неожиданные виды. Например, несколько лет назад среди молодых девушек прокатилась волна тренда на маленькие цилиндрики, которые носили в качестве аксессуара на головном ободке.

— Цилиндр — это образ жизни. Сейчас это часть жизни и винтажной игры людей, которые любят появиться в цилиндре на вечеринке и каком-то мероприятии. Вряд ли цилиндр вернётся в повседневную жизнь людей. Но жаль, ведь головные уборы — великая вещь. То, что начали от них отказываться, не придаёт облику человека значительности.

Видео:Осевая и силовая проба (Подбор астигматизма)Скачать

Цилиндр в архитектуре

Презентация полезна тем, что показывает повсеместное архитектурное использование фигуры цилиндр.

Содержимое разработки

Государственное бюджетное профессиональное образовательное учреждение

«Ковровский медицинский колледж имени Е. И. Смирнова»

Специальность: «Акушерское дело»

Подготовил студент 05 – А группы

В современном мире в архитектуре начинается использование всё более новых, сложных и интересных фигур. Людям становится скучно жить среди однообразных пятиэтажных домов. Моё внимание привлёк цилиндр. Фигура не простая сама по себе, а применить её в строительстве – сложно и неоднозначно. В моей презентации я хочу рассказать Вам о том, что же такое цилиндр, поведаю о некоторых его особенностях и покажу на примере его использование в одной из главных наук мира – архитектуре.

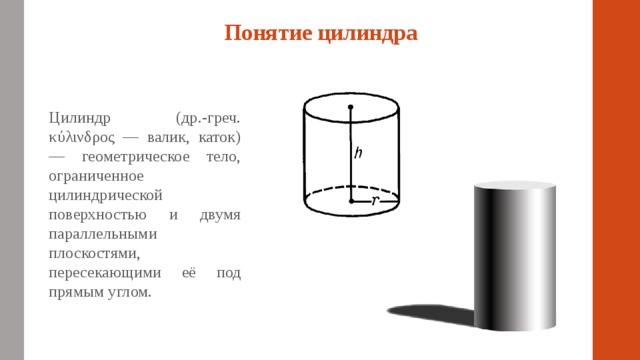
Цилиндр (др.-греч. κύλινδρος — валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её под прямым углом.

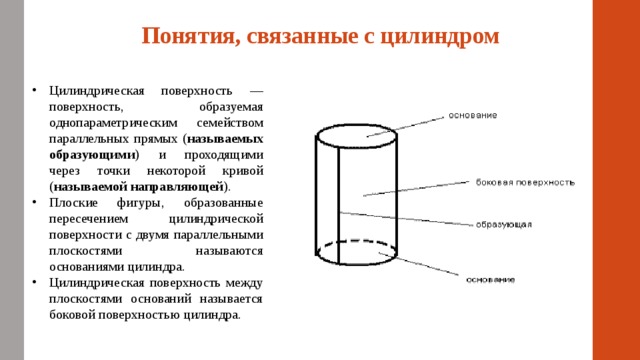
Понятия, связанные с цилиндром

Цилиндрическая поверхность — поверхность, образуемая однопараметрическим семейством параллельных прямых ( называемых образующими ) и проходящими через точки некоторой кривой ( называемой направляющей ).
Плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями называются основаниями цилиндра.
Цилиндрическая поверхность между плоскостями оснований называется боковой поверхностью цилиндра.

Хронология цилиндра в архитектуре

Цилиндры в древней архитектуре

Сами цилиндры появились в архитектуре ещё в древние века, они выступали в роли несущих и второстепенных элементов. Конечно, всё началось с округлых колонн. Их применяли всё время и такой архитектурных ход был распространён. Здания же цилиндрической формы появились лишь в наше время.

Читайте также: Объем кругового сегмента цилиндра

Первые каменные колонны применили в Древнем Египте при постройке Пирамиды Джосера в 2650 году до н.э. Впервые в истории была применена каменная постройка из 40 колонн высотой каждой из них в 10 метров. Так как эти колонны были первыми на земле, архитектор Имхотеп соединил каждую из них со стеной с одной стороны.

Также одни из самых популярных сооружений цилиндрической формы является Колизей в Риме.

Цилиндры в современной архитектуре

Среди компонентов современной архитектуры можно найти немало кубических конструкций (особенно из стекла), треугольников в виде, например, фронтонов; и случайные изгибы тоже часто встречаются. Но что насчёт цилиндров? При их упоминании в связи со строительством зданий вспоминается стиль арт-деко, который весьма недолго был популярен в начале 20 века.

Цилиндры и закруглённые углы использовались им для передачи динамики плавных движений. В поле ретроспективы также оказываются башенки средневековых сооружений и примитивные промышленные здания Америки.

Тем не менее, цилиндры нашли себе место в современной архитектуре. Редкие образцы производят сильнейшее впечатление, если перекликаются с контекстом.

Есть два вопроса, отсутствие ответов на которые, объясняет нежелание архитекторов включать цилиндрические формы в структуру зданий, тем более жилых. Что будет находиться внутри? И как связать цилиндр с остальной частью здания эмоционально и физически?

По первому пункту можно заметить, что внутри цилиндров обычно возводятся лестницы, которые наполняют всю конструкцию практическим смыслом. Что касается второго вопроса, здесь будут продемонстрированы здания, смежные стены которых разделены цилиндрическим элементом, который может выдаваться вперёд или стоять вровень с фасадом.

Ещё с древних времен люди использовали в строительстве цилиндрические формы зданий. Мы убедились, что непросто выбрать такой сложной фигуре своё место в архитектурном пространстве. Но, хоть это и сложно, выглядит потрясающе!

Видео:определение силы цилиндраСкачать

Презентация по геометрии на тему «Цилиндр и его элементы»(11 класс)

Ищем педагогов в команду «Инфоурок»

Описание презентации по отдельным слайдам:

муниципальное автономное общеобразовательное учреждение средняя общеобразовательная школа № 45 Методическое пособие для учащихся 11 классов Составил учитель математики высшей категории Гавинская Елена Вячеславовна. г.Калининград 2016-2017 учебный год

В древности при строительстве грандиозных храмов и дворцов людям приходилось таскать и носить на себе огромные валуны и колонны. Тогда и было замечено, что катать предметы намного легче и удобнее. Примерно так и появились и популяризовались цилиндры. И по сей день эти тела вращения часто встречаются в нашей жизни. В архитектуре, в технике, в мире моды – цилиндры побывали везде.

Определение. Цилиндр (греч. kýlindros, валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью (называемой боковой поверхностью цилиндра) и не более чем двумя поверхностями (основаниями цилиндра).

Другие определения цилиндра. Цилиндр — это фигура, состоящая из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Цилиндром называется тело, ограниченное замкнутой цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими эту поверхность. У Евклида цилиндр получается вращением прямоугольника. У Кавальери – движением образующей (при произвольной направляющей – «цилиндрика»).

Вклад Евклида в математику. О Евклиде почти ничего неизвестно, откуда он был родом, где и у кого учился. Папп Александрийский (III в.) сообщает, что он был очень доброжелателен ко всем тем, кто сделал хоть какой-нибудь вклад в математику, корректен, в высшей степени порядочен и совершенно лишен тщеславия. Евклид, как и другие великие греческие геометры, занимался астрономией, оптикой и теорией музыки. До нас дошли его сочинения, посвященные прикладным вопросам: «Феномены» (элементарная сферическая астрономия), «Оптика» (учение о перспективе) и «Сечение канона» ( теория музыки). Это были первые прообразы будущих исследований по математической физике: в них теория выводилась строго дедуктивно из явно сформулированных физических гипотез и математических постулатов. Гораздо больше мы знаем о математическом творчестве Евклида. Прежде всего Евклид является для нас автором «Начал», по которым учились математики всего мира. Эта удивительная книга пережила более двух тысячелетии, но до сих пор не утратила своего значения не только в истории науки, но и самой математике. Созданная там система евклидовой геометрии и теперь изучается во всех школах мира и лежит в основе почти всей практической деятельности людей. На геометрии Евклида базируется классическая механика, ее апофеозом было появление в 1687 г. Математических начал натуральной философии Ньютона, где законы земной и небесной механики и физики устанавливаются в абсолютном евклидовом пространстве. Содержание «Начал» далеко не исчерпывается элементарной геометрией — это основы всей античной математики. Здесь подводится итог более чем 300-летнему ее развитию и вместе с тем создается прочная 6aзa для дальнейших исследований. Последующие математики ссылались на предложения «Начал», как на нечто окончательно установленное.

Читайте также: Как проверить работоспособность цилиндра сцепления ваз 2106

Вклад Кавальери в математику. В своем основном труде «Геометрия» (1635г.) Кавальери развил разработанный им задолго до выхода книги новый метод определения площадей и объемов – так называемый метод неделимых. Неделимыми Кавальери называл параллельные между собой хорды плоской фигуры или параллельные плоскости тела. Важнейший признак неделимости состоит в том, что число измерений его на единицу меньше самого геометрического образа. У плоской фигуры 2 измерения, у ее неделимого, т.е. у отрезка – 1 измерение. Кавальери доказал теорему о том, что площади двух подобных фигур относятся как квадраты, а объемы – как кубы соответствующих неделимых, и установил, что отношение суммы квадратов всех неделимых треугольника к сумме квадратов всех неделимых параллелограмма, имеющего с треугольником одинаковые основания и высоту, равно 1:3. Впоследствии Кавальери нашел аналогичные соотношения для суммы кубов и т.д. до девятой степени неделимых. Труды Кавальери сыграли огромную роль в формировании исчисления бесконечно малых.

Элементы цилиндра. Круги, ограничивающие цилиндрическую поверхность называются основаниями цилиндра. Отрезки образующих, заключенные между основаниями, называются образующими цилиндра, а образованная ими поверхность – боковой поверхностью цилиндра. Ось цилиндрической поверхности называется осью цилиндра.

Свойства цилиндра. Основания равны и параллельны. Образующие равны и параллельны. Все сечения цилиндра плоскостями, параллельными плоскостям оснований цилиндра, равны основаниям цилиндра.

1. Основания циилиндра равны и параллельны. Справедливость этого утверждения следует из того, что множество концов образующих, лежащих в плоскости β, получается из окружности L параллельным переносом на вектор ОО1. Параллельный перенос является движением и, значит, наложением, а при наложении любая фигура переходит в равную ей фигуру. Следовательно, при параллельном переносе на вектор ОО1 окружность L перейдет в равную ей окружность L1 радиуса r с центром в точке О1. Доказательства свойств. α β L L1 о о1

2. Образующие цилиндра равны и параллельны. Все образующие цилиндра перпендикулярны к плоскостям оснований. Но плоскости оснований цилиндра параллельны. Значит, все образующие цилиндра – расстояния между параллельными плоскостями, следовательно, (по теореме) они равны и параллельны.

3. Все сечения цилиндра плоскостями, параллельными плоскостям оснований цилиндра, равны основаниям цилиндра. Действительно, любое такое сечение является общим основанием двух цилиндров, на которые секущая плоскость разбивает данный цилиндр. Поэтому оно равно другим основаниям этих цилиндров, которые являются основаниями исходного цилиндра.

Влияние оснований на цилиндр. Если основания цилиндра плоские (и, следовательно, содержащие их плоскости параллельны), то цилиндр называют стоящим на плоскости. Если основания стоящего на плоскости цилиндра перпендикулярны образующей, то цилиндр называется прямым. В частности, если основание стоящего на плоскости цилиндра — круг, то говорят о круговом (круглом) цилиндре; если эллипс — то эллиптическом. α β

Виды цилиндра. Бесконечное тело, ограниченное замкнутой бесконечной цилиндрической поверхностью, называется бесконечным цилиндром. Прямой круговой цилиндр — это поверхность, образованная вращением одной из параллельных прямых вокруг другой, принятой в качестве оси вращения. Бесконечное тело, ограниченное замкнутым цилиндрическим лучом и его основанием, называется открытым цилиндром. Основание и образующие цилиндрического луча называют соответственно основанием и образующими открытого цилиндра. Конечное тело, ограниченное замкнутой конечной цилиндрической поверхностью и двумя выделившими её сечениями, называется конечным цилиндром, или собственно цилиндром. Сечения называются основаниями цилиндра. По определению конечной цилиндрической поверхности, основания цилиндра равны.