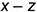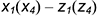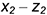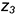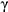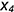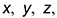Присмотритесь к окружающим нас предметам. Многие из них имеют форму геометрических тел или их сочетаний.
Форма деталей, встречающихся в технике, также представляет собой сочетание различных геометрических тел или их частей. Например, ось (рис. 124, а) образована в результате добавления к одному цилиндру другого цилиндра, меньшего по размерам, а втулка (рис. 124, б) получилась после того, как из цилиндра удалили другой цилиндр меньшего диаметра.
Рис. 124. Деталь как суумма или разность геометрических тел
Форма каждого геометрического тела и его изображений на чертеже имеет свои характерные признаки. Этим пользуются, чтобы облегчить чтение и выполнение чертежей.
Деталь мысленно расчленяют на отдельные составляющие ее части, имеющие изображения, характерные для известных нам геометрических тел.
Мысленное расчленение предмета на составляющие его геометрические тела называется анализом геометрической формы.
Из каких геометрических тел состоит деталь, изображенная на рис. 125?
Рис. 125. Заготовка ключа
Форма детали состоит из усеченного конуса, цилиндра, куба, цилиндра, части шара (рис. 126, а). Из большего цилиндра удален элемент цилиндрической формы.
После такого анализа форму детали представить легче (рис. 126, б). Поэтому необходимо знать характерные особенности проекций геометрических тел.
Рис. 126. Анализ геометрической формы заготовки ключа: а — элементы детали; б — общий вид детали
Цилиндр и конус. Проекции цилиндра и конуса показаны на рис. 127, а и б. Круги, лежащие в основаниях цилиндра и конуса, расположены параллельно горизонтальной плоскости проекций; проекции оснований на горизонтальную плоскость будут также кругами.
Фронтальная и профильная проекция цилиндра — прямоугольники, а конуса — равнобедренные треугольники.
На рис. 127в, дан чертеж усеченного конуса, горизонтальная проекция которого представляет собой две окружности, а фронтальная проекция — равнобочную трапецию.
Выполнение чертежей цилиндра и конуса начинают с проведения осей симметрии.
Из рис. 127, а видно, что фронтальная и профильная проекции цилиндра одинаковы. То же можно сказать о проекциях конуса. Поэтому в данном случае профильные проекции на чертеже лишние. На рисунке они даны лишь для того, чтобы показать, какую форму имеют все три проекции цилиндра и конуса.
Размеры цилиндра и конуса определяются высотой h и диаметром основания d. Для усеченного конуса указывают высоту h и диаметры обоих оснований D и d.
Рис. 127. Цилиндр и конус: а, б и в — комплексные чертежи; построения изометрической проекции; г, д и е — последовательность
Знак диаметра ∅ позволяет определять форму предмета и по одной проекции (рис. 128).
Рис. 128. Рациональное выполнение изображений цилиндра и конуса
Для построения изометрической проекции цилиндра и конуса (см. рис. 127, г и д) проводят оси х и у, на которых строят ромб со стороной, равной диаметру предмета, в ромб вписывают овал (построение овала см. рис. 96); вдоль оси z откладывают высоту предмета. Для цилиндра и усеченного конуса строят второй овал и проводят касательные к овалам.
Куб и прямоугольный параллелепипед. При проецировании куб располагают так, чтобы его грани были параллельны плоскостям проекций. Тогда на параллельных плоскостях грани изобразятся в натуральную величину, т. е. квадратами, а на перпендикулярных плоскостях — прямыми линиями. Проекциями куба являются три равных квадрата (рис. 129, а).
Построение изометрической проекции куба показано на рис. 129, в.
Прямоугольный параллелепипед проецируется подобно кубу. На рис. 129, б приведены три его проекции — прямоугольники.
На чертеже куба и параллелепипеда проставляют три размера: длину, высоту и ширину.
Рис. 129. Куб и прямоугольный параллелепипед: а и б — комплексные чертежи; в — последовательность построения изометрической проекции
На рис. 130, а приведено наглядное изображение детали, а на рис. 130, б дан ее чертеж. Деталь состоит из двух прямоугольных параллелепипедов, имеющих по две квадратные грани. Обратите внимание, как проставлены на чертеже размеры.
Рис. 130. Рациональное выполнение чертежа
Применение условного знака □ позволило вычертить деталь в одной проекции. Тонкие пересекающиеся линии на чертеже означают, что отмеченные ими поверхности — плоские.
Правильные треугольная и шестиугольная призмы. Основания призм, параллельные горизонтальные плоскости проекций, изображаются на ней в натуральную величину, а на фронтальной и профильной плоскостях — в виде прямых линий. Боковые грани изображаются в натуральную величину на плоскостях проекций, которым они параллельны, и в виде линий на тех плоскостях, которым они перпендикулярны (рис. 131, а и б). Грани, наклонные к плоскостям проекций, изображаются искаженными.
Видео:ПИРАМИДА в ИЗОМЕТРИИСкачать
Рис. 131. Правильные призмы: а и б — комплексные чертежи; в и г — последовательность построения изометрической проекции
Размеры призм определяются высотой и размерами фигуры основания. Штрихпунктирными линиями на чертежах проводят оси симметрии.
Построение изометрии призм (рис. 131, в и г) начинают с основания. Затем из каждой вершины основания восставляют перпендикуляры, откладывают на них высоту и проводят линии, параллельные ребрам основания.
Выполнение чертежей начинают также с горизонтальной проекции.
Правильная четырехугольная пирамида. Квадратное основание пирамиды проецируется на горизонтальную плоскость в натуральную величину. На проекции основания пирамиды диагоналями изображаются боковые ребра, идущие от вершин основания к вершине пирамиды (рис. 132, а). Фронтальная и профильная проекции пирамиды — равнобедренные треугольники.
Читайте также: Как проверить главный тормозной цилиндр ваз 2109
Размеры пирамиды определяются длиной b двух сторон основания и высотой h.
Построение изометрической проекции пирамиды (рис. 132, б) начинают с основания. Затем из центра полученной фигуры восставляют перпендикуляр, откладывают на нем высоту и соединяют полученную точку с вершинами основания.
Рис. 132. Правильная пирамида: а — комплексный чертеж; б — последовательность построения изометрической проекции
Шар. Все проекции шара (рис. 133) — круги, диаметр которых равен диаметру шара. На каждой проекции проводят центровые линии.
Рис. 133. Комплексный чертеж шара
Тор. На рис. 134, а даны две проекции тора (кругового кольца). На фронтальной проекции в натуральную величину изображается окружность, в результате вращения которой образуется тор. Горизонтальная проекция представляет собой две концентрические окружности. Радиус внешней окружности больше радиуса внутренней на величину, равную диаметру образующей окружности.
Рис. 134. Тор: а — две проекции; б — деталь, имеющая торовые поверхноти
Размеры тора определяются диаметром (или радиусом) образующей окружности и внутренним (или наружным) диаметром кольца. На всех проекциях проводят оси симметрии. Среди поверхностей детали, изображенной на рис. 134, б, есть две торовые поверхности. Радиус образующей окружности одного тора 16 мм, другого — 12 мм.
- Задания к § 19
- Примеры построения аксонометрических проекций
- Примеры построения аксонометрических проекций
- Построение аксонометрии пирамиды выполняется по предлагаемому графическому алгоритму
- Построение аксонометрии выполняется по аналогичному графическому алгоритму
- Построение аксонометрии выполняется по следующему графическому алгоритму
- Построение аксонометрии выполняется по следующему графическому алгоритму
- Построение аксонометрии призмы выполняется по следующему графическому алгоритму
- 🎥 Видео
Ответьте на вопросы
1. В чем заключается анализ геометрической формы предметов? Каково его значение?
2. Что общего и в чем отличие между проекциями цилиндра и конуса?
3. Какую форму имеют проекции куба и прямоугольного параллелепипеда?
4. Что означают тонкие пересекающиеся линии на проекции предмета ?
5. Какую форму имеют проекции правильной треугольной и шестиугольной призм, правильной четырехугольной пирамиды?
6. Сколькими и какими размерами определяется величина цилиндра, конуса, куба, параллелепипеда, правильных треугольной и шестиугольной призм, правильной четырехугольной пирамиды, шара, тора?
7. Для каких геометрических тел при наличии размеров можно ограничиться одной проекцией?
8. У каких геометрических тел все проекции одинаковы?
Задания к § 19
Упражнение 62
Запишите в рабочей тетради наименования и размеры геометрических тел, на которые можно расчленить формы деталей (рис. 135, а и б).
Форма записи:
Упражнение 63
Вычертите по три проекции и выполните технические рисунки следующих геометрических тел: цилиндра, конуса, правильных треугольной и шестиугольной призм и пирамиды. При выполнении чертежей не забудьте провести осевые и центровые линии. Правильно нанести размеры, следуя примерам, данным на рис. 127, а и б; 131, а и б; 135, а. Величину деталей определите обмериванием изображений на этих рисунках. Чертежи выполните в масштабе 5 : 1.
Упражнение 64
Пользуясь конструктором для моделирования А. Н. Сальникова, сложите указанные Вам преподавателем модели, привете денные на рис. 136, а — з. (Конструктор для моделирования A. H. Сальникова состоит из элементов, представляющих собой геометрические тела или их части. Он входит в комплект оборудования кабинета черчения.) При отсутствии конструктора изготовьте модели из дерева, пенопласта или другого материала.
Рис. 136. Задания на моделирование
Упражнение 65
Видео:Как начертить цилиндр в объемеСкачать

Рассмотрите чертежи, приведенные на рис. 137, а — в, и ответьте на следующие вопросы применительно к каждому чертежу:
Рис. 137. Задания для упражнений
1. Какие виды даны на чертеже?
2. Из каких геометрических тел состоит деталь?
3. Каковы размеры каждого геометрического тела?
4. Какова шероховатость поверхностей детали? Выполните чертежи геометрических тел, на которые можно расчленить деталь, и технический рисунок детали.
Упражнение 66
Начертите деталь по описанию, приведенному ниже, и нанесите на чертеж размеры.
Деталь имеет форму цилиндра диаметром 35 мм. В центре одного горца просверлено глухое отверстие диаметром 20 и длиной 30 мм. Другой конец детали — квадратная призма. Размеры основания призмы 24 х 24 мм, высота ее 30 мм. Общая длина детали 90 мм. Шероховатость всех поверхностей соответствует Rz 25.
Упражнение 67
Чертежи деталей на рис. 138 содержат один, два или три вида. Запишите в рабочей тетради, какие чертежи выполнены наиболее рационально, и объясните почему.
Форма записи:
Рис. 138. Задания на определение рациональности чертежа
Примеры построения аксонометрических проекций
Примеры построения аксонометрических проекций
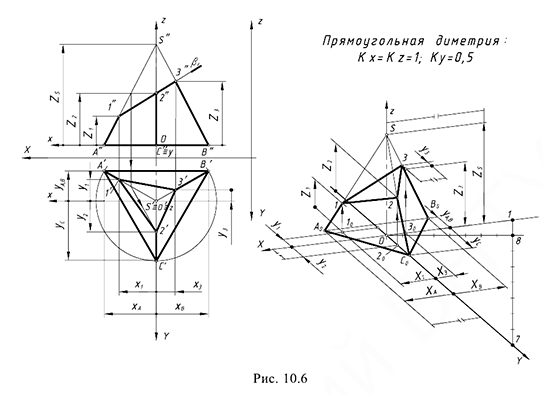
На рис. 10.6 показан пример построения аксонометрической проекции правильной треугольной пирамиды со срезом фронтально-проецирующей плоскостью в прямоугольной диметрии.
Построение аксонометрии пирамиды выполняется по предлагаемому графическому алгоритму
1-е действие. Отнести пирамиду к системе прямоугольных координат 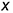
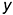
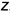
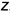
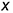
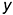
2-е действие. Определить в принятой системе координат на проекциях пирамиды координаты 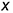
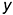
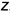
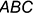
3-е действие. На свободном поле чертежа провести аксонометрические оси прямоугольной диметрии из произвольной точки 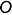
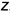
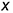
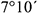
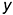
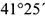
4-е действие. Построить тонкими линиями аксонометрическую проекцию пирамиды без среза.
4.1. Построить аксонометрическое изображение основания пирамиды 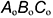
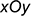
- точка
: координатная ломаная
;
- точка
: координатная ломаная
,
- точка
.
. Координатные отрезки параллельны соответствующим аксонометрическим осям.
4.2. Построить по координате 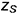
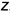
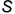
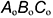
Читайте также: Цилиндр isotec шелл all
5-е действие. Достроить срез на аксонометрии пирамиды, построив на ребрах пирамиды по координатам 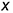
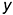
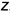
- точка 1 на ребре
: координатная ломаная —
- точка 2 на ребре
;
- точка 3 на ребре
.
6-е действие. Оформить аксонометрию пирамиды, выполнив толстыми линиями ее видимый контур (оставить тонкими линиями полную проекцию пирамиды, невидимые линии и линии построения).
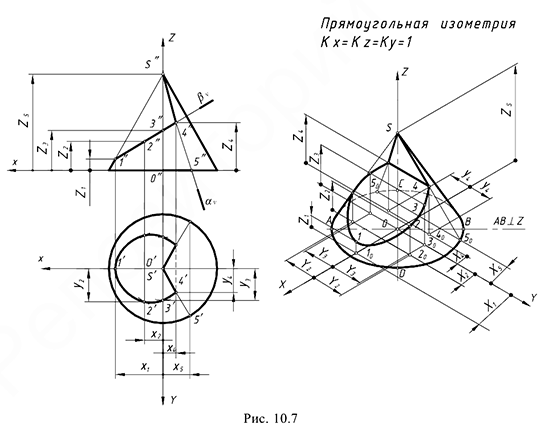
На рис. 10.7 показан пример построения аксонометрической проекции конуса со срезами двумя фронтально-проецирующими плоскостями (в сечении плоскостью 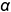
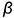
Графические действия для построения аксонометрии конуса соответствуют предложенному алгоритму для построения аксонометрии пирамиды:
1-е действие. Отнести конус к такой же системе прямоугольных координат 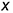
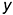
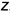
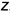
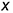
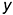
2-е действие. Определить координаты 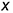
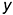
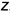
3-е действие. На свободном поле чертежа отметить точку 
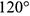
Видео:Построение аксонометрии моделиСкачать

4-е действие. Построить аксонометрическую проекцию конуса без срезов:
4.1. Построить эллипс основания конуса с центром в точке 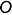
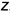
4.2. Построить вершину конуса точку 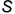
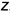
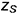
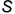
5-е действие. Достроить срезы на аксонометрии конуса, построив аксонометрические проекции отмеченных точек 1, 2, 3 и 4 по соответствующим плоским координатным ломаным:
- точка 1: координатная ломаная
;
- точки 2: координатная ломаная
- точки 3: координатная ломаная
;
- точки 4: координатная ломаная
(лежат на образующих
).
Соединить построенные точки соответствующими линиям (участок эллипса и треугольник).
6-е действие. Оформить чертеж аксонометрии конуса, выполнив толстыми линиями ее видимый контур (оставить тонкими линиями полный контур пирамиды, невидимые линии и линии построения).
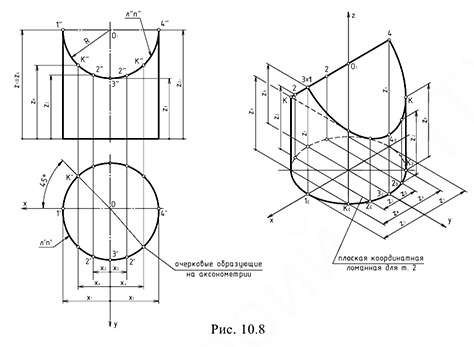
На рис. 10.8 показано построение аксонометрической проекции цилиндра с полуцилиндрическим вырезом (их радиусы равны) в прямоугольной изометрии.
В этом частном случае пересечения поверхностей для построения линии пересечения на профильной проекции следует применить теорему Г. Монжа, так как эти две цилиндрические поверхности 2-го порядка равных диаметров описаны вокруг сферы.
Построение аксонометрии выполняется по аналогичному графическому алгоритму
1-е действие. Отнести цилиндр к системе координатных осей 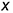
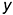
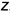
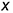
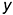
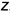
2-е действие. Обозначить характерные и промежуточные точки 1, 2, 3 и 4 на поверхности цилиндра и определить координаты 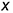
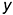
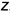
3-е действие. На свободном поле чертежа отметить точку 
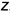
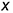
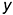
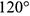
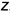
4-е действие. Построить аксонометрию цилиндра без выреза.
4.1. Построить эллипс нижнего основания цилиндра в точке 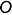
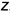
4.2. Построить точку 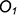
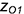
5-е действие. Достроить вырез на аксонометрии цилиндра, построив проекции обозначенных точек 1, 2, 3 и 4 по координатным ломаным (снизу вверх) :
• точки 1 и 4 —> ;
• точки 2 —> (четыре точки);
• точки 3 —> (две точки);
• точки 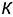
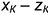
• построенные точки соединить:
- одна плоская кривая проецируется на аксонометрию в виде эллипса;
- вторая плоская кривая проецируется в прямую линию (запомните!).
6-е действие. Соедините построенные точки соответствующими линиями — отрезками образующих и участками эллипсов.
7-е действие. Оформить аксонометрию цилиндра, выполнив толстыми линиями ее видимый контур (оставить тонкими линиями полный контур цилиндра, невидимые линии и линии построения).
На рис. 10.9 показан пример построения шара со срезами в прямоугольной изометрии.
Напомним, что сечением поверхности шара любой плоскостью является окружность. Но на чертеже окружности проецируются в эллипсы. В примере срезы выполнены профильной плоскостью 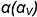
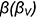
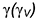
• эллипс окружности , лежащий в профильной плоскости;
• эллипс окружности , лежащий в горизонтальной плоскости;
• эллипс как проекцию окружности, лежащий в плоскости , по обозначенным точкам.
Аксонометрическим изображением шара в прямоугольной изометрии является окружность с диаметром, равным 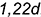
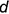
Графический алгоритм для построения аксонометрии шара следующий:
Видео:Как начертить КОНУС С ВЫРЕЗОМ (чертеж + аксонометрия)Скачать

1-е действие. Отнести шар к системе координат 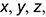
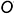
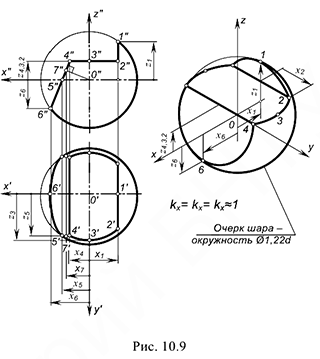
2-е действие. Обозначить характерные точки 1, 2, 3, 4, 5 и б на поверхности шара и определить координаты обозначенных точек для построения срезов на аксонометрии.
3-е действие. На свободном поле чертежа отметить точку начала аксонометрических координат и провести аксонометрические оси прямоугольной изометрии.
4-е действие. Построить аксонометрию шара без срезов — провести окружность диаметром .
5-е действие. Достроить срезы на аксонометрии шара:
• построить эллипс диаметром 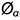
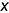
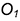
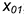
• построить эллипс диаметром 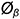
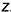
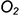
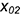
Читайте также: Шлифовка блока цилиндров газель
• построить по координате линию 4-4 на построенном горизонтальном эллипсе;
• построить по координатам точки 5 и 6: точку 5 — по ломаной 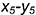
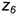
6-е действие. Соединить построенные точки 4-5-6 эллиптической кривой.
7-е действие. Оформить аксонометрию шара, выполнив толстыми линиями его видимый контур, оставив тонкими линиями полный очерк шара, невидимые линии и линии построения.
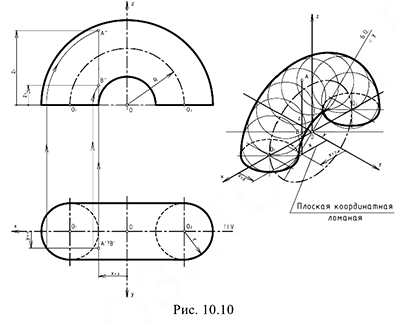
На рис. 10.10 показан пример построения половины открытого тора в прямоугольной изометрии.
Построение аксонометрии выполняется по следующему графическому алгоритму
1-е действие. Отнести тор к системе координат .
2-е действие. Если тор со срезами, обозначить характерный точки и определить их координаты: например, координаты точек 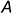
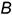
3-е действие. На свободном поле чертежа отметить точку начала аксонометрических координат и провести аксонометрические оси прямоугольной изометрии.
4-е действие. Построить эллипс направляющей окружности радиусом 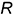
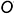
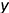
5-е действие. В полученных на оси 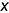
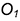
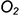
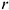
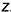
6-е действие. Построить аксонометрию тора:
• провести достаточное количество образующих окружностей диаметрами, равными с центрами на эллипсе направляющей окружности тора;
• провести две лекальные огибающие касательные кривые.
7-е действие. Достроить аксонометрические проекции заданных точек 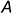
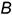
• точка
• точка
8-е действие. Оформить аксонометрию открытого тора.
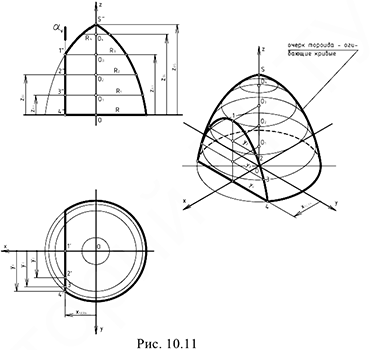
На рис. 10.11 показан пример построения тороида (самопересекающегося тора) в прямоугольной изометрии.
Построение аксонометрии выполняется по следующему графическому алгоритму
1-е действие. Отнести тор к системе координат проходящей по его основанию и ось вращения.
2-е действие. Рассечь тороид достаточным количеством плоскостей, перпендикулярных оси его вращения и определить радиус окружности каждого сечения (измерить линейкой) с центрами в точках 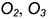
3-е действие. Обозначить характерные точки 1, 2, 3 и 4 среза и определить их координаты.
Видео:Аксонометрические проекцииСкачать

4-е действие. На свободном поле чертежа отметить точку начала аксонометрических координат и провести аксонометрические оси прямоугольной изометрии.
5-е действие. Построить аксонометрию тороида:
• построить семейство эллипсов в точках 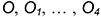
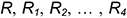
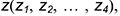
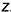
• построить точку ;
• провести две касательные огибающие кривые к эллипсам.
6-е действие. Достроить срез на аксонометрии тороида по координатам отмеченных точек (построения см. рис. 10.11).
7-е действие. Оформить аксонометрию тороида.
. Аксонометрическая проекция глобоида в прямоугольной изометрии строится аналогично тем же способом «сечений».
На рис. 10.12 показан пример построения аксонометрической проекции правильной четырехгранной призмы со сквозным пазом, выполненным двумя профильными 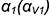
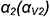
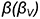
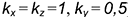
Построение аксонометрии призмы выполняется по следующему графическому алгоритму
1-е действие. Отнести («привязать») призму к системе прямоугольных координат 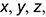
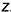
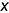
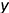
2-е действие. Обозначить характерные точки 1, 2, …, 5 на поверхности призмы.
3-е действие. Определить в отнесенной к призме системе координат на ее проекциях координаты обозначенных точек:
• точки 1 и 5, лежащих на верхнем основании и ребрах призмы;
• точек 2 и 4, лежащих на линиях пересечения плоскостей паза, а также обозначенных буквами 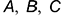
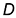
4-е действие. На свободном поле чертежа отметить точку О начала аксонометрических координат и провести аксонометрические оси косоугольной диметрии: ось 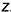
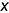
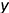
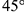
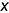
5-е действие. Построить тонкими линиями аксонометрическую проекцию призмы без выреза:
5.1. Построить нижнее основание призмы 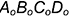
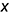
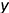
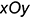
• точки 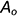
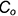
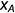
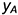
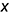
• точки 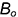
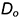
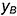
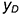
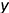
• соединить построенные вершины отрезками прямых линий.
5.2. Построить верхнее основание призмы:
• отложить от точки 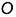
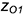
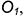
• из точек 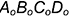
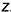
6-е действие. Достроить на аксонометрии призмы вырез по координатам обозначенных точек (сверху вниз):
• точки 1 и 5 на верхнем основании по координатам 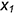
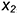
• точки 2 и 4 — на вертикальных линиях, параллельных оси 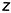
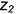
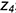
• точки 3- на ребрах 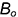
7-е действие. Соединить построенные точки отрезками прямых линий.
8-е действие. Оформить аксонометрию призмы, выполнив толстыми линиями ее видимый контур; оставить тонкими линиями полную проекцию призмы, невидимые линии и линии построения.
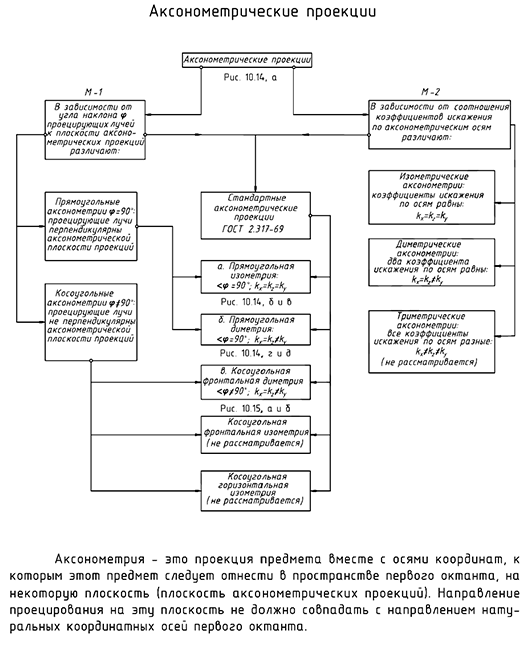
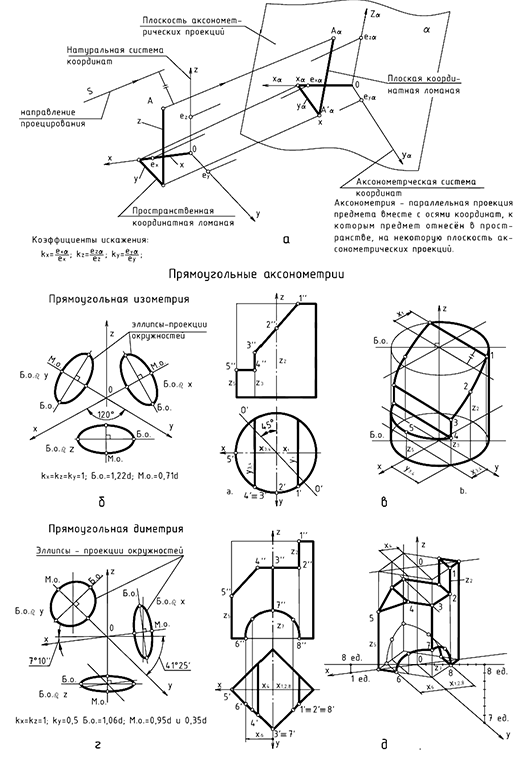
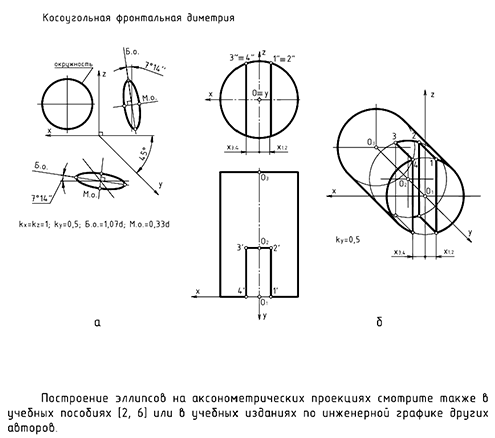
Структуризация материала десятой лекции в рассмотренном объеме схематически представлена на рис. 10.13 (лист 1). На последующих листах 2 и 3 компактно приведены иллюстрации к этой схеме для визуального закрепления основной части изученного материала при повторении (рис. 10.14 и 10.15).
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Возможно эти страницы вам будут полезны:




















































Видео:Задание 38. Как начертить ИЗОМЕТРИЮ усеченного цилиндраСкачать

Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🎥 Видео
Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Как начертить конус в объемеСкачать
Топографическое черчение. Аксонометрические проекции. Цилиндр (15.01.2016)Скачать

2 Построение шестигранной призмы и пирамиды в аксонометрииСкачать

Цилиндр, вытянутый вдоль оси Z. Урок33.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать
Аксонометрические проекцииСкачать

2 3 Чертеж и изометрия пирамиды пятиугольнойСкачать

2 2 3 построение изометрии окружностиСкачать

Черчение. 7 класс. Тема: Аксонометрические проекции. Видеоинструкция по заданию от 10.02Скачать

Как начертить аксонометрию. Наглядный пример. Уроки черчения.Скачать

Построение изометрии цилиндраСкачать

Аксонометрические проекции.Скачать

Шестиугольная пирамида.Ортогональные и изометрическая проекции.Урок31.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

конусСкачать


























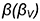
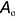 : координатная ломаная
: координатная ломаная  ;
;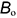 : координатная ломаная
: координатная ломаная 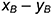 ,
,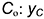 .
. : координатная ломаная —
: координатная ломаная — 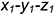
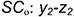 ;
;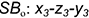 .
.
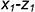 ;
;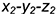
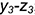 ;
;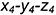 (лежат на образующих
(лежат на образующих 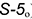 ).
).