В цилиндр вписан правильный тетраэдр со стороной

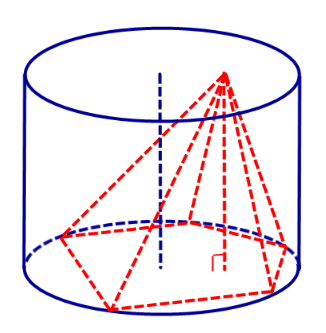
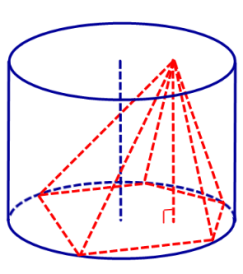
Одна вершина правильного тетраэдра расположена на оси цилиндра, а другие вершины – на боковой поверхности цилиндра. Найдите ребро тетраэдра, если радиус основания цилиндра равен R .

Решение

Пусть вершина A правильного тетраэдра ABCD расположена на оси цилиндра, а вершины B , C и D – на его боковой поверхности. Рассмотрим ортогональные проекции B 1 , C 1 и D 1 точек соответственно B , C и D на ось цилиндра. Из равенства прямоугольных треугольников ABB 1 , ACC 1 и ADD 1 следует равенство отрезков AB 1 , AC 1 и AD 1 , расположенных на оси цилиндра. Поэтому либо точки B 1 , C 1 и D 1 совпадают, либо две из них совпадают, а третья симметрична им относительно вершины A . В первом случае (рис.1) плоскость, проходящая через вершины B , C и D , лежащие на боковой поверхности цилиндра, перпендикулярна оси. Тогда равносторонний треугольник BCD вписан в окружность радиуса R . Следовательно, его сторона равна R . Во втором случае (рис.2) только одна сторона равностороннего треугольника BCD перпендикулярна оси конуса. Предположим, что это сторона BC . Обозначим через a ребро тетраэдра. Пусть K – середина BC , P – точка пересечения прямой B 1K с образующей цилиндра, проходящей через точку D (рис.3). Рассмотрим осевое сечение цилиндра, проходящее через точку D . Получим прямоугольник DD 1B 1P , в который вписан равнобедренный треугольник ADK , причём A – середина B 1D 1 ,
DD 1 = B 1P = R, AD = a, AK = DK = .
Из прямоугольных треугольников AD 1D , AB 1K и DPK находим, что
AD 1 = = ,

= = ,
а т.к. B 1P = B 1K + KP , получим уравнение
R = + ,
из которого находим, что a = .

Ответ

Источники и прецеденты использования

Проект осуществляется при поддержке и .

Видео:Правильный тетраэдр вписан в цилиндр. Математика ЕГЭСкачать

В цилиндр вписан правильный тетраэдр со стороной

Внутри правильного тетраэдра с ребром a‍ расположены четыре равных шара. Каждый шар касается трёх других и трёх граней тетраэдра. Найдите радиусы шаров.

Пусть r —‍ искомый радиус. Соединим попарно центры шаров. Получим правильный тетраэдр со стороной 2r.‍ Так как шары вписаны в трёхгранные углы при вершинах правильного тетраэдра, то их центры лежат на соответствующих высотах тетраэдра. Поэтому центр правильного тетраэдра с вершинами в центрах данных шаров совпадает с центром O‍ данного правильного тетраэдра.

Пусть шар радиуса r‍ с центром O‍₁,‍ вписанный в трёхгранный угол с вершиной D,‍ касается плоскости грани ABD‍ данного правильного тетраэдра ABCD‍ со стороной a‍ в точке P.‍

Пусть M —‍ центр основания ABC,‍ K —‍ середина AB,‍ φ —‍ угол между высотой тетраэдра и плоскостью его грани. Из прямоугольного треугольника DMK‍ находим, что

Значит, или откуда находим, что

Видео:Видеоурок по математике "Цилиндр"Скачать

Пирамида, вписанная в цилиндр

Видео:Математика ЕГЭ. В цилиндр вписан правильный тетраэдрСкачать

Пирамида, вписанная в цилиндр. Свойства пирамиды, вписанной в цилиндр

Определение 1. Пирамидой, вписанной в цилиндр, называют такую пирамиду, у которой основание вписано в одно из оснований цилиндра, а вершина лежит на другом основании цилиндра (рис. 1).

Определение 2. Если пирамида вписана в цилиндр, то цилиндр называют описанным около пирамиды.

Читайте также: Насадка для хонинговки цилиндров

Замечание. Если пирамида вписана в цилиндр, то высота пирамиды равна высоте цилиндра.

Из определения пирамиды, вписанной в цилиндр, легко вытекает следующее утверждение, доказательство которого мы оставляем читателю.

Утверждение. Около любой правильной пирамиды можно описать цилиндр.

Видео:не растачивайте цилиндры пока не посмотрите это видео!Скачать

Отношение объемов цилиндра и вписанной в него правильной n — угольной пирамиды

Задача. Найти отношение объемов цилиндра и вписанной в него правильной n — угольной пирамиды.

Решение. Поскольку объем цилиндра вычисляется по формуле

а объем пирамиды вычисляется по формуле

Поскольку площадь правильного n — угольника выражается через радиус R описанной около этого многоугольника окружности по формуле

Следствие 1. Отношение объема правильной треугольной пирамиды к объему цилиндра, описанного около данной пирамиды, равно

Следствие 2. Отношение объема правильного тетраэдра к объему цилиндра, описанного около данного тетраэдра, равно

Следствие 3. Отношение объема правильной четырехугольной пирамиды к объему цилиндра, описанного около данной пирамиды, равно

Следствие 4. Отношение объема правильной шестиугольной пирамиды к объему цилиндра, описанного около данной пирамиды, равно

Видео:Найдите координаты всех вершин правильного тетраэдраСкачать

В цилиндр вписан правильный тетраэдр со стороной

Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.

Радиусы шара и основания цилиндра равны. Площадь поверхности цилиндра, с радиусом основания r и высотой 2r равна

Площадь поверхности шара радиуса r равна то есть в 1,5 раза меньше площади поверхности цилиндра. Следовательно, площадь поверхности шара равна 12.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому сторона основания равна 8, а площадь основания равна 64. Тогда высота цилиндра равна

Почему получилось 64? Что-то не понятно:(

Длина диаметра цилиндра равна длине стороны квадрата в основании.

В куб вписан шар радиуса 1. Найдите объем куба.

Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:

В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

По теореме Пифагора длина гипотенузы треугольника в основании Поскольку гипотенуза является диаметром основания описанного цилиндра, его объем

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

В цилиндр вписан правильный тетраэдр со стороной

Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.

Радиусы шара и основания цилиндра равны. Площадь поверхности цилиндра, с радиусом основания r и высотой 2r равна

Площадь поверхности шара радиуса r равна то есть в 1,5 раза меньше площади поверхности цилиндра. Следовательно, площадь поверхности шара равна 12.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому сторона основания равна 8, а площадь основания равна 64. Тогда высота цилиндра равна

Почему получилось 64? Что-то не понятно:(

Длина диаметра цилиндра равна длине стороны квадрата в основании.

В куб вписан шар радиуса 1. Найдите объем куба.

Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:

В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

Читайте также: Нет компрессии в трех цилиндрах причины

По теореме Пифагора длина гипотенузы треугольника в основании Поскольку гипотенуза является диаметром основания описанного цилиндра, его объем

Видео:Бюджетный способ лечения задировСкачать

Сфера, вписанная в цилиндр

Ищем педагогов в команду «Инфоурок»

Описание презентации по отдельным слайдам:

Описание слайда:

Сфера, вписанная в цилиндр
Сфера называется вписанной в цилиндр, если она касается его оснований и боковой поверхности (касается каждой образующей). При этом цилиндр называется описанным около сферы.
В цилиндр можно вписать сферу, если высота цилиндра равна
диаметру его основания.
Ее центром будет точка O, являющаяся
серединой отрезка, соединяющего центры оснований O1 и O2 цилиндра.
Радиус сферы R будет равен
радиусу окружности основания цилиндра.

Описание слайда:

Упражнение 1
В цилиндр высоты 2 вписана сфера. Найдите ее радиус.
Ответ: 1.

Описание слайда:

Упражнение 2
В цилиндр вписана сфера радиуса 1. Найдите высоту цилиндра.
Ответ: 2.

Описание слайда:

Упражнение 3
Радиус основания цилиндра равен 2. Какой должна быть высота цилиндра, чтобы в него можно было вписать сферу?
Ответ: 4.

Описание слайда:

Упражнение 4
Высота цилиндра равна 2. Каким должен быть радиус основания цилиндра, чтобы в него можно было вписать сферу?
Ответ: 1.

Описание слайда:

Упражнение 5
Осевым сечением цилиндра является прямоугольник со сторонами 1 и 2. Можно ли в этот цилиндр вписать сферу?
Ответ: Нет.

Описание слайда:

Упражнение 6
Осевым сечением цилиндра является квадрат. Можно ли в этот цилиндр вписать сферу?
Ответ: Да.

Описание слайда:

Упражнение 7
Можно ли вписать сферу в цилиндр, осевым сечением которого является ромб?
Ответ: Нет.

Описание слайда:

Упражнение 8
Можно ли вписать сферу в наклонный цилиндр?
Ответ: Нет.

Описание слайда:

Упражнение 9
Площадь осевого сечения цилиндра, в который вписана сфера, равна 4 см2. Найдите диаметр сферы.
Ответ: 2 см.

Описание слайда:

Упражнение 10
Периметр осевого сечения цилиндра, в который вписана сфера, равен 8 см. Найдите радиус сферы.
Ответ: 1 см.

Описание слайда:

Упражнение 11
Какой наибольший радиус может быть у сферы, помещающейся в цилиндр, радиус основания которого равен 2, и высота 1.
Ответ: 0,5 см.

Описание слайда:

Упражнение 12
Можно ли сферу радиуса 1 поместить в наклонный цилиндр, радиус основания которого равен 1, а боковое ребро равно 2 и наклонено к плоскости основания под углом 60о.
Ответ: Нет.

Описание слайда:

Упражнение 13
Какой наибольший радиус может быть у сферы, помещающейся в наклонный цилиндр, радиус основания которого равен 1, а боковое ребро равно 2 и наклонено к плоскости основания под углом 60о.
Ответ:

Описание слайда:

Сфера, описанная около цилиндра
Цилиндр называется вписанным в сферу, если окружности оснований цилиндра лежат на сфере. При этом сфера называется описанной около цилиндра.
Около любого цилиндра можно описать сферу. Ее центром будет точка O, являющаяся серединой отрезка, соединяющего центры оснований O1 и O2 цилиндра.
Радиус сферы R вычисляется по формуле

где h – высота цилиндра, r – радиус окружности основания.

Описание слайда:

Упражнение 1
Диагональ осевого сечения цилиндра равна 2. Найдите радиус сферы, описанной около этого цилиндра.
Ответ: 1.

Описание слайда:

Упражнение 2
Около цилиндра высоты 2 и радиуса основания 1 описана сфера. Найдите ее радиус.
Ответ:

Описание слайда:

Упражнение 3
Около цилиндра, радиус основания которого равен 1, описана сфера радиуса 2. Найдите высоту цилиндра.
Ответ:

Описание слайда:

Упражнение 4
Около цилиндра, высота которого равна 1, описана сфера радиуса 1. Найдите радиус основания цилиндра.
Ответ:

Описание слайда:

Упражнение 5
Найдите наименьший радиус сферы, в которую помещается наклонный цилиндр, радиус основания которого равен 1, образующая равна 2 и наклонена к плоскости основания под углом 60о.
Ответ:

Описание слайда:

Цилиндр, вписанный в призму
Цилиндр называется вписанным в призму, если его основания вписаны в основания цилиндра. При этом, призма называется описанной около цилиндра
В призму можно вписать цилиндр тогда и только тогда, когда
в ее основание можно вписать окружность.
Радиус основания цилиндра равен
радиусу окружности, вписанной в основание призмы.
Высота цилиндра равна
высоте призмы.

Описание слайда:

Упражнение 1
Можно ли вписать цилиндр в наклонную призму?
Ответ: Да, наклонный цилиндр.

Читайте также: Нумерация цилиндров шевроле лачетти

Описание слайда:

Упражнение 2
В основании прямой призмы правильный треугольник со стороной 1. Найдите радиус окружности основания цилиндра, вписанного в эту призму.
Ответ:

Описание слайда:

Упражнение 3
В основании прямой призмы прямоугольный треугольник с катетами 6 и 8. Найдите радиус окружности основания цилиндра, вписанного в эту призму.
Ответ: 2.

Описание слайда:

Упражнение 4
Найдите радиус окружности основания цилиндра, вписанного в единичный куб.
Ответ:

Описание слайда:

Упражнение 5
В правильную шестиугольную призму, со стороной основания 1, вписан цилиндр. Найдите радиус окружности основания этого цилиндра.
Ответ:

Описание слайда:

Цилиндр, описанный около призмы
Цилиндр называется описанным около призмы, если его основания описаны около оснований цилиндра. При этом, призма называется вписанной в цилиндр
Около призмы можно описать цилиндр, если около ее оснований можно описать окружности.
Высота цилиндра равна
высоте призмы.
радиусу окружности, описанной около основания призмы.
Радиус основания цилиндра равен

Описание слайда:

Упражнение 1
Можно ли описать цилиндр около наклонной призмы?
Ответ: Да, наклонный цилиндр.

Описание слайда:

Упражнение 2
В основании прямой призмы правильный треугольник со стороной 1. Найдите радиус окружности основания цилиндра, описанного около этой призмы.
Ответ:

Описание слайда:

Упражнение 3
В основании прямой призмы прямоугольный треугольник с катетами 6 и 8. Найдите радиус окружности основания цилиндра, описанного около этой призмы.
Ответ: 5.

Описание слайда:

Упражнение 4
В основании прямой призмы квадрат со стороной 1. Найдите радиус окружности основания цилиндра, описанного около этой призмы.
Ответ:

Описание слайда:

Упражнение 5
Около правильной шестиугольной призмы, со стороной основания 1, описан цилиндр. Найдите радиус окружности основания этого цилиндра.
Ответ: 1.

Описание слайда:

Упражнение 6
Около единичного тетраэдра описан цилиндр так, что вершины тетраэдра принадлежат окружностям оснований цилиндра. Найдите радиус основания и высоту цилиндра.
Ответ:

Описание слайда:

Упражнение 7
Около единичного октаэдра описан цилиндр так, что две противоположные вершины октаэдра находятся в центрах оснований цилиндра, а остальные вершины принадлежат боковой поверхности цилиндра. Найдите радиус основания и высоту цилиндра.
Ответ:

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

Курс повышения квалификации

Охрана труда

Курс профессиональной переподготовки

Охрана труда

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Международная дистанционная олимпиада Осень 2021

Похожие материалы

Урок по математике «Геометрические фигуры. Признаки и характеристики предметов»

Сценарий открытого мероприятия, посвящённого 75-летию Победы в Великой Отечественной войне: «Памяти павших будьте достойны!»

Возможности и риски педагогической диагностики

Презентация на тему : «Этологическая теория»

Мастер-класс для воспитателей «Нетрадиционные техники лепки»

Презентация на тему: Электрический ток. Анализ опасности поражения током

«Вред и польза жевательной резинки»

Статья «Нетрадиционные формы обучения столяров»

Воспользуйтесь поиском по нашей базе из
5244630 материалов.

Вам будут интересны эти курсы:

Оставьте свой комментарий

В школе в Пермском крае произошла стрельба

Школьных охранников предлагают обучать основам психологии

Минпросвещения объявило конкурс «Учитель-международник»

Минпросвещения намерено включить проверку иллюстраций в критерии экспертизы учебников

Школьников не планируют переводить на удаленку после каникул

Рособрнадзор оставил за регионами решение о дополнительных школьных каникулах

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📽️ Видео

11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Стереометрия | Комбинация телСкачать

РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

Профильный ЕГЭ 2024. Вся стереометрия первой части. Задача 3. МиниСИРОПСкачать

✓ Задача про цилиндр | ЕГЭ-2018. Задание 14. Математика. Профильный уровень | Борис ТрушинСкачать

ЗАДИРОВ в цилиндрах НЕ БУДЕТ если делать так...Скачать

11 класс, 32 урок, Объем цилиндраСкачать

27. Стереометрия на ЕГЭ по математике. Задача на тему: Отношение объемов подобных тел .Скачать

ЗАДАНИЕ 2 ЕГЭ (ПРОФИЛЬ). ЦИЛИНДР.Скачать

Задание 5. ЕГЭ профиль. КОМБИНАЦИИ ТЕЛ.Скачать

Объём цилиндраСкачать

Комбинации тел. Урок 10. Геометрия 11 классСкачать