Вычислить площадь части цилиндра вырезанной плоскостями (4 видео)

Площадь S плоской области D в прямоугольных координатах вычисляется по формуле:

Пример. Вычислить площадь области, ограниченной линиями и у = х + 6.

Решение: Найдем точки пересечения данных линий, для этого решим систему уравнений:

Решением будет пара значений (-3; 9) и (-2; 4) — координаты точек пересечения графиков

Область D запишем в виде системы неравенств

Согласно формуле (1), получим

Вычисление объема тела

Видео:60. Площадь поверхности цилиндраСкачать

Объем цилиндрического тела, ограниченного сверху поверхностью z=f(x, у), снизу плоскостью z = 0 и сбоку прямой цилиндрической поверхностью, вырезающей на плоскости xOy (z = 0) область D , вычисляется по формуле

Пример. Вычислить объем тела, ограниченного поверхностями z = 2x+1, x= 0, у = 4,

Решение:Тело, ограниченное заданными поверхностями, представляет собой вертикальный параболический цилиндр, расположенный в I октанте. Сверху тело ограничено плоскостью z = 2x+1, сбоку параболическим цилиндром у =x и плоскостями х = 0 и у = 4, снизу

параболой у =x и прямыми х = 0 и у = 4. Найдем точки пересечения параболы у =x и прямой у = 4:

Получаем два решения: (-2; 4) и (2; 4). Значение не рассматриваем, т.к. цилиндр расположен в I октанте. Область D запишем в виде системы неравенств 0 ≤ x ≤ 2, x ≤ y ≤ 4. Согласно формуле (3), получим

Пример. Вычислить объем тела, ограниченного поверхностями

Решение: Данное тело есть прямой круговой цилиндр, ограниченный сверху плоскостью

, а снизу — кругом в плоскости z=0. Область D в основании цилиндра запишем в виде системы неравенств

Согласно формуле (3), получим

Первый интеграл табличный и равен:

Читайте также: Зазор поршень цилиндр 4д56

Видео:Площадь сферы внутри цилиндра. Поверхностный интегралСкачать

Второй интеграл вычисляется подстановкой ;следовательно, второй интеграл равен:

Вычисление площади поверхности

Если поверхность задана уравнением z=f(x, у) и проектируется в область D плоскости хОу (z = 0), то площадь S поверхности вычисляется по формуле

Если поверхность проектируется на плоскость yOz (x = 0), то уравнение поверхности следует решить относительно переменной х и формула примет вид

Если поверхность проектируется на плоскость хОу(у = 0), то уравнение поверхности следует решить относительно переменной у и формула примет вид

Пример.Вычислить площадь треугольника, образованного при пересечении плоскости

x + 3y + 2z = 6 с координатными плоскостями.

Решение: найдем отрезки, отсекаемые на координатных осях данной плоскостью:

Чтобы воспользоваться формулой (4), решим уравнение данной плоскости относительно переменной z и найдем частные производные:

Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

При z = 0 имеем х + 3у = 6, откуда ; следовательно, в плоскости z = 0 область D запишется в виде системы неравенств

Пример. Вычислить площадь части поверхности цилиндра , заключенной между плоскостями z = 0, z = 4x, y = 0.

Решение: искомая поверхность лежит в I октанте. Проекция поверхности на плоскость xOz (у = 0) есть прямоугольный треугольник, в котором ОА=х = 4 и уравнение гипотенузы OВ имеет вид z = 4x. Следовательно, область D в плоскости xOz определяется системой неравенств 0 ≤ x ≤ 4, 0 ≤ z ≤ 4x

Поскольку заданная поверхность спроектирована на плоскость xOz, для вычисления площади поверхности применим формулу (6). Из уравнения цилиндра получим

Находим частные производные:

Тогда Для вычисления последнего интеграла применили подстановку .

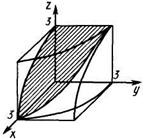
Пример. Вычислить площадь части поверхности цилиндра , вырезанной цилиндром .

Решение:искомая поверхность образована пересечением двух цилиндров и . В эти уравнения поверхностей входят квадраты переменных, поэтому искомая поверхность симметрична относительно каждой из координатных плоскостей и для вычисления рассмотрим 1/8 ее часть, лежащую в I октанте.

Читайте также: Главный тормозной цилиндр тойота калдина ст 210

Видео:Площадь фигурыСкачать

Область интегрирования D представляет собой 1/4 часть круга , заключенного между положительными полуосями Ох и Оу, и определяется системой неравенств

Из уравнения имеем . Далее, находим частные производные

1. Вычислите площадь фигуры, ограниченной линиями ;

2. Вычислите объем тела, ограниченного поверхностями

3. Вычислите площадь части поверхности цилиндра , ограниченного плоскостями

1. Вычислите площадь фигуры, ограниченной гиперболой и прямой ;

2. Вычислите объем тела, ограниченного поверхностями

3. Вычислите площадь части поверхности цилиндра у = х 2 + 2, ограниченного плоскостями

1. Вычислите площадь фигуры, ограниченной линиями

2. Вычислите объем тела, ограниченного поверхностями

Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

3. Вычислите площадь части поверхности цилиндра , ограниченного плоскостями z = 0, z = 8;

1. Вычислите площадь фигуры, ограниченной линиями

2. Вычислите объем тела, ограниченного

3. Вычислите площадь части поверхности цилиндра , ограниченного плоскостями z = 0, z = 2x, y = 0, x = 0.

1. Назовите формулу для вычисления площади плоской фигуры;

2. Как найти объем цилиндрического тела, ограниченного сверху поверхностью z=f(x, у), снизу плоскостью z = 0 и сбоку прямой цилиндрической поверхностью, вырезающей на плоскости xOy (z = 0) область D?

3. По какой формуле вычисляется площадь S поверхности, если поверхность задана уравнением

z=f(x, у) и проектируется в область D плоскости хОу (z = 0)?

5.5 Необходимые расчеты. Анализ результатов расчетов

5.7 Ответы на контрольные вопросы

1. Колягин Ю.М. , Луканкин Г.Л., Яковлев Г.Н. Математика в 2-х томах: Учебное пособие — М. Новая волна, 2005, 2 кн., с. 453-457;

2. Подольский В. А. Сборник задач по математике: Учебное пособие — М. Высшая школа, 2003, с.375-381;